Căn bậc ba là gì? Cách tìm căn bậc ba và bài tập vận dụng
 27/06/2023 - admin
27/06/2023 - admin
Để giúp các em hiểu về căn bậc ba là gì? Cách tìm căn bậc ba? Phương pháp giải các bài tập chi tiết nhất? Đội ngũ THPT Lê Hồng Phong với bài viết này sẽ làm rõ hơn cho các em những vấn đề trên để các em có thể nắm rõ những kiến thức căn bản liên quan đến căn bậc ba.
1. Căn bậc ba là gì?
Trước khi đi vào làm bài tập vận dụng ta cần hiểu rõ hơn về phần lý thuyết sau đây:
Căn bậc ba của một số thực a là số thực x sao cho x³ = a.
Kí hiệu: ![]()
Chú ý:
- Mọi số thực đều có duy nhất một căn bậc ba.
- Căn bậc ba của số dương là số dương
- Căn bậc ba của số âm là số âm
- Căn bậc ba của số 0 là số 0.
2. Cách tìm căn bậc ba của một số
Muốn tìm căn bậc ba của một số a thì ta xem bao nhiêu mũ ba lên thì bằng a.
Ví dụ 1: Tìm căn bậc ba của một số dương
![]()
Ví dụ 2: Tìm căn bậc ba của một số âm
![]()
Ví dụ 3: Tìm căn bậc ba của một phân số
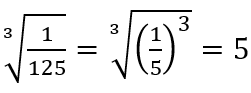
3. Các công thức liên quan đến phép tính căn bậc ba
A) Công thức liên quan

B) Cách trục căn thức bậc ba
Ta áp dụng 2 hằng đẳng thức đã học
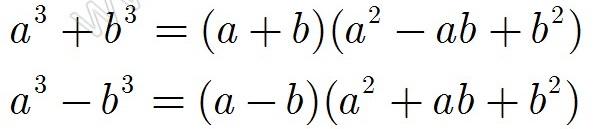
>> Xem thêm tổng hợp kiến thức liên quan đến căn bậc hai
4. Các dạng bài tập
Dạng 1: Tính căn bậc ba
Ví dụ: Tính
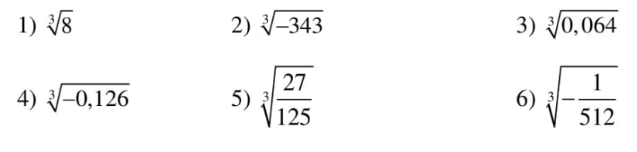
Hướng dẫn giải bài tập:
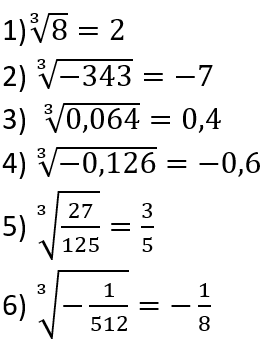
Dạng 2: So sánh 2 căn
Phương pháp giải:
- Đưa hai biểu tức cần so sánh về dạng cơ bản

- Áp dụng tính chất cơ bản suy ra kết quả.
- Những bài không thể đưa ngay về dạng cơ bản thì có thể lập phương hai biểu thức đã cho rồi so sánh: Nếu

Ví dụ 1: So sánh ![]() và
và ![]()
Hướng dẫn giải: ![]()
Ví dụ 2: So sánh ![]() và
và ![]()
Hướng dẫn giải:
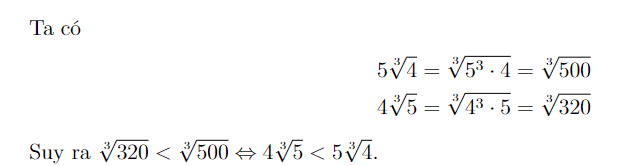
Dạng 3: Rút gọn biểu thức
Phương pháp giải:
Dùng các phép biến đổi đưa biểu thức dưới dấu căn về dạng ![]() hoặc mũ 3 cả hai vế của biểu thức đưa về giải phương trình bậc ba
hoặc mũ 3 cả hai vế của biểu thức đưa về giải phương trình bậc ba
Ví dụ: Rút gọn biểu thức
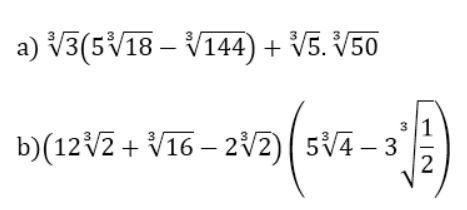
Hướng dẫn giải:
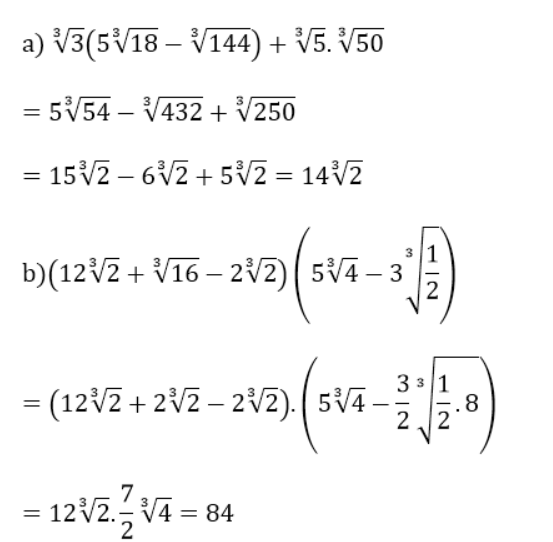
Dạng 4: Giải phương trình chứa căn bậc ba
Phương pháp giải
Lũy thừa bậc ba hai vế của phương trình rồi đưa về dạng phương trình tích hoặc ta có thể đặt ẩn phụ
Ví dụ: Giải các phương trình sau
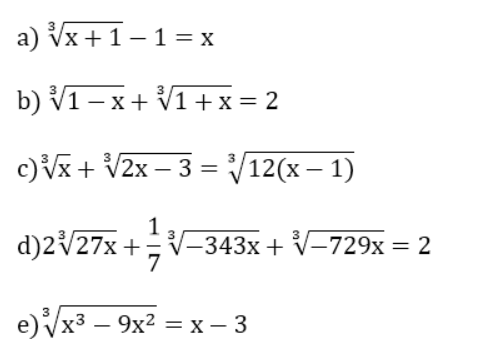
Hướng dẫn giải:


Bài tập tự luyện
Bài 1: Tính

Bài 2 : So sánh
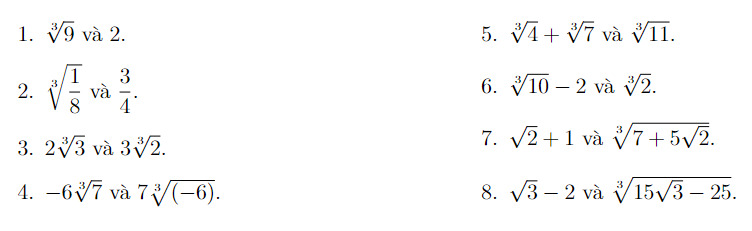
Bài 3: Rút gọn biểu thức
![]()
Bài 4: Rút gọn biểu thức
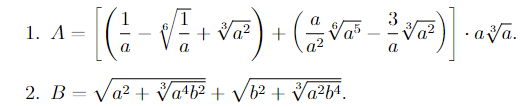
Bài 5 Giải các phương trình
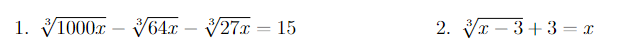
Trên là tất cả những kiến thức liên quan đến căn bậc ba mà đội ngũ THPT Lê Hồng Phong tổng hợp lại được. Mong rằng với bài viết trên các em sẽ có cái nhìn căn bản về bài học. Và đừng quên theo dõi chúng tôi để không bỏ lỡ các bài viết liên quan đến Toán 9 hay những môn học khác nhé.