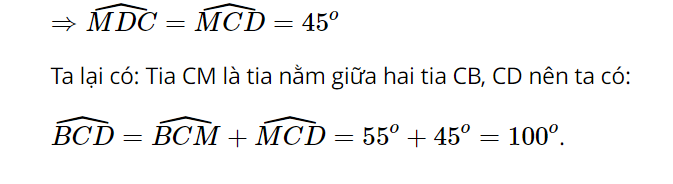Tứ giác nội tiếp? Lý thuyết, bài tập vận dụng

Tứ giác nội tiếp là một hình học có bốn đỉnh nằm trên cùng một đường tròn. Nhằm giúp các em nắm bắt được bài học và phục vụ cho quá trình ôn thi vào lớp 10, bài viết này của THPT Lê Hồng Phong sẽ tổng hợp chi tiết về lý thuyết và bài tập liên quan đến bài học. Cùng theo dõi ngay nhé!

I. Lý thuyết vè tứ giác nội tiếp

1. Khái niệm về tứ giác nội tiếp

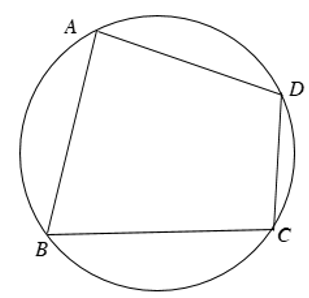
Một tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (gọi tắt là tứ giác nội tiếp)

2. Định lý

+ Trong một tứ giác nội tiếp, tổng số đo hai góc đối diện bằng 180°.

+ Nếu một tứ giác có tổng số đo hai góc đối diện bằng 180° thì tứ giác đó nội tiếp được đường tròn.

Tứ giác ABCD nội tiếp đường tròn (O), suy ra

3. Dấu hiệu nhận biết tứ giác nội tiếp

+ Tứ giác có tổng hai góc đối bằng 180°.

+ Tứ giác có góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện.

+ Tứ giác có bốn đỉnh cách đều một điểm (mà ta có thể xác định được). Điểm đó là tâm của đường tròn ngoại tiếp tứ giác đó.

+ Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh chứa hai đỉnh còn lại dưới một góc α.

+ Chú ý: Để chứng minh một tứ giác là tứ giác nội tiếp ta có thể chứng minh tứ giác đó là một trong các hình sau: Hình chữ nhật, hình vuông, hình thang cân.

II. Bài tập minh họa

Bài 53 – 89 SGK Toán 9 Tập 2:

Biết ABCD là tứ giác nội tiếp. Hãy điền vào ô trống trong bảng sau (nếu có thể ):

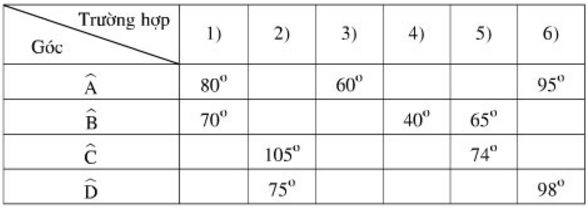
Lời giải

Tứ giác nội tiếp có tổng hai góc đối bằng 180⁰ nên:

– Điền vào ô trống:

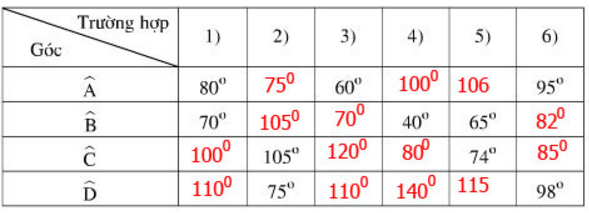
– Cách tính:

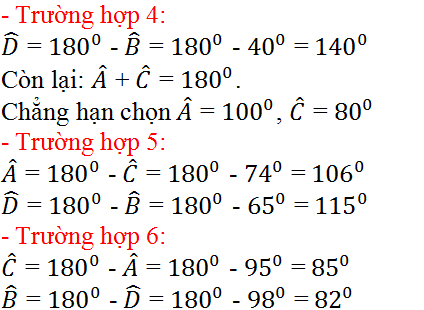
Bài 54 – 89 SGK Toán 9 Tập 2:

Tứ giác ABCD có góc ABC + góc ADC = 180^o. Chứng minh rằng các đường trung trực của AC, BD, AB cùng đi qua một điểm.

Lời giải

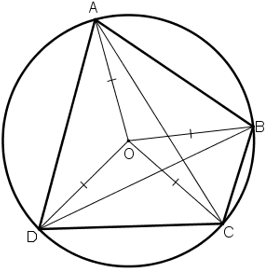
Tứ giác ABCD có

⇒ ABCD là tứ giác nội tiếp

Gọi O là tâm đường tròn ngoại tiếp tứ giác ABCD

⇒ OA = OB = OC = OD = R

Do OA= OC nên ΔOAC cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AC.

Do OB= OD nên ΔOBD cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của BD

Do OA= OB nên ΔOAB cân tại O, đường trung tuyến kẻ từ O cũng chính là đường cao của tam giác. Suy ra, O thuộc đường trung trực của AB.

⇒ O thuộc đường trung trực của AC, BD, AB .

Vậy các đường trung trực của AC, BD, AB cùng đi qua O.

Bài 55 – 89 SGK Toán 9 Tập 2:

Cho ABCD là một tứ giác nội tiếp đường tròn tâm M, biết: Hãy tính số đo các góc

Lời giải