Thấu Kính Phân Kỳ? Cách vẽ, công thức, Bài Tập Áp Dụng

Chuyên đề thấu kính phân kỳ là chuyên đề quan trọng thường gặp trong các bài thi của các em. Bài viết sau sẽ giúp các em nắm rõ về thấu kính phân kỳ là gì? Cách vẽ thấu kính, công thức, bài tập áp dụng. Cùng theo dõi ngay!

1. Thấu kính phân kỳ là gì?

Thấu kính phân kì hay còn được gọi là thấu kính rìa dày, là một khối chất trong suốt (thường bằng nhựa hoặc thủy tinh), đồng chất và được giới hạn bởi một mặt lõm kết hợp một mặt phẳng. Ngoài ra, thấu kính phân kì cũng có thể được giới hạn bởi hai mặt lõm.

2. Đặc điểm của thấu kính phân kỳ

2.1 Hình dạng thấu kính phân kỳ

Thấu kính phân kỳ thường có ít nhất hai bề mặt cong khác nhau để tạo ra hiệu ứng phân kỳ.

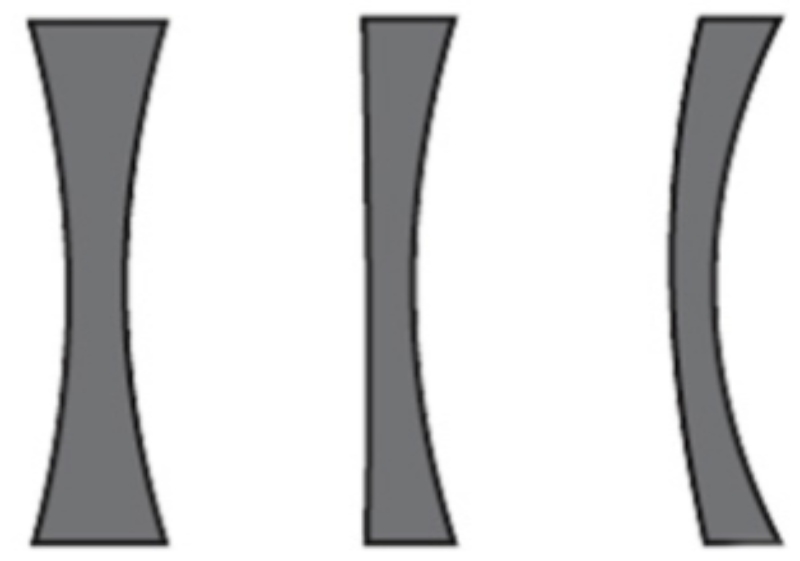
Bề mặt lồi của thấu kính phân kỳ thường có bán kính cong dương (+), trong khi bề mặt lõm có bán kính cong âm (-). Đặc điểm này giúp tạo ra sự khác biệt về chỉ số khúc xạ của các bề mặt và tạo ra hiệu ứng phân kỳ khi ánh sáng đi qua.

2.2 Tia sáng qua thấu kính phân kỳ

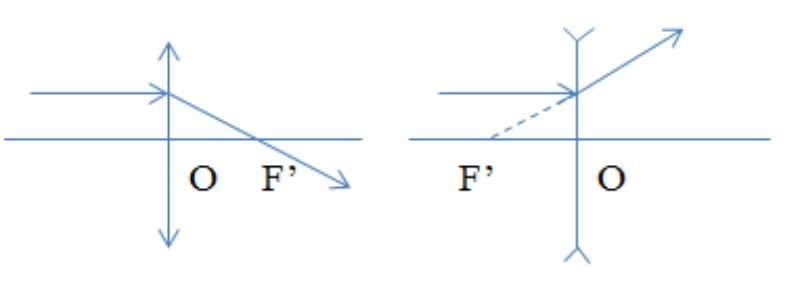
Khi chiếu một chùm tia tới song song với trục của thấu kính và theo phương vuông góc với mặt của thấu kính đó, sẽ xuất hiện chùm tia ló phân kì.

Tia sáng khi đi qua thấu kính phân kỳ sẽ trải qua quá trình khúc xạ và chuyển hướng. Góc chuyển hướng của tia sáng phụ thuộc vào góc tiếp xúc ban đầu với bề mặt thấu kính và các thông số hình học của thấu kính như bán kính cong và độ cong.

3. Trục chính, quang tâm, tiêu điểm, tiêu cự của thấu kính hội tụ

3.1 Trục chính của thấu kính phân kỳ

Giống như thấu kính hội tụ trục chính của một thấu kính phân kỳ là đường thẳng đi qua trung tâm của thấu kính và vuông góc với các bề mặt cong của nó. Trục chính là đường thẳng mà tia sáng đi qua mà không bị chuyển hướng hoặc giao thoa sau khi đi qua thấu kính.

Đối với một thấu kính phân kỳ lõm, trục chính đi qua trung tâm của cả hai bề mặt lõm. Trục chính cũng sẽ chia thấu kính thành hai phần đối xứng.

3.2 Quang tâm thấu kính phân kỳ

quang tâm của một thấu kính phân kỳ là một điểm đặc biệt trên trục chính của thấu kính. Quang tâm được ký hiệu bằng chữ “O”. Quang tâm của thấu kính là nơi mà tia sáng song song và tiếp tục đi theo trục chính của thấu kính sau khi đi qua thấu kính.

Khi một tia sáng song song đi vào thấu kính phân kỳ, nó sẽ bị chuyển hướng và giao điểm tại quang tâm. Điều này tạo ra hiệu ứng phân kỳ và tập trung ánh sáng tại điểm tiêu điểm sau khi đi qua thấu kính.

3.3 Tiêu điểm, tiêu cự của thấu kính

– Tiêu điểm của một thấu kính phân kỳ là vị trí mà các tia sáng song đi qua thấu kính sau khi đã bị lăn xạ. Đối với thấu kính phân kỳ hội tụ, tiêu điểm nằm ở một vị trí xa thấu kính, trong khi đối với thấu kính phân kỳ phân tán, tiêu điểm nằm ở một vị trí gần thấu kính.

– Tiêu cự của một thấu kính phân kỳ là khoảng cách từ tiêu điểm tới trung tâm thấu kính. Nó có thể được đo từ bề mặt tiếp xúc với chất lăng kính hoặc từ trung tâm hình cầu của thấu kính. Tiêu cự thường được ký hiệu bằng chữ f.

4. Cách vẽ thấu kính phân kỳ

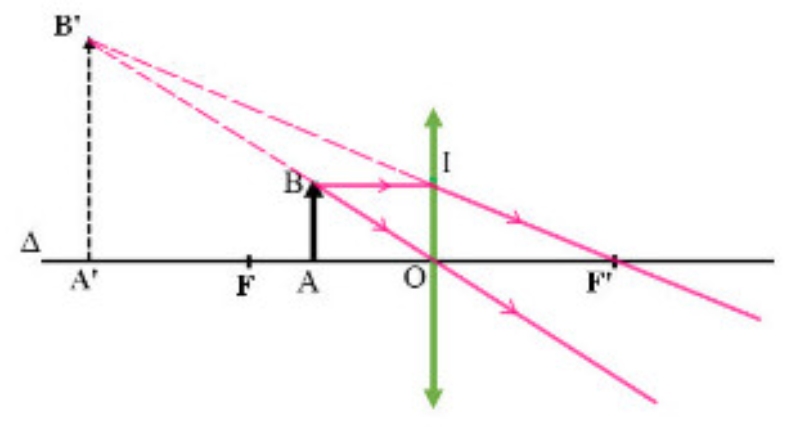
• B1: Vẽ tia song song với trục chính của thấu kính (tia số 1) thu được tia ló đi qua có phần kéo dài đi qua tiêu điểm F’ (tiêu điểm ảnh của thấu kính phân kì).
• B2: ẽ tiếp tia đi qua quang tâm O của thấu kính (tia số 2) thu được tia ló truyền thẳng qua O
  B3: Giao điểm của tia số 1 và tia số 2 là điểm B’ ảnh của điểm B. Từ B’ hạ vuông góc xuống trục chính của thấu kính => điểm A’

Lưu ý: ảnh của vật thật qua thấu kính phân kì luôn là ảnh ảo

5. Công thức tính

• Công thức liên hệ giữa vị trí của vật, vị trí của ảnh và tiêu cự của thấu kính

Qui ước dấu:

– Thấu kính hội tụ: f > 0

– Thấu kính phân kỳ: f < 0

– ảnh là thật: d’ > 0

– ảnh là ảo: d’ < 0

– vật là thật: d > 0

•  Công thức số phóng đại của thấu kính

Qui ước dấu:

–  k > 0: ảnh và vật cùng chiều

–  k < 0: ảnh và vật là ngược chiều

•  Công thức tính độ tụ của thấu kính

Trong đó:

– n: chiết suất của chất làm thấu kính

– R₁; R₂: bán kính của các mặt cong (R = ∞ cho trường hợp mặt phẳng) (m)

– D: độ tụ của thấu kính (dp đọc là điốp)

– f: tiêu cự của thấu kính (m)

6. Bài tập vận dụng

Bài tập 1

Một vật sáng AB có dạng mũi tên đặt vuông góc trục chính của thấu kính phân kỳ, cho ảnh cao 3,6 cm và cách thấu kính 6cm. Thấu kính có tiêu cự 15 cm.
a. Xác định kích thư
b. và vị trí của ảnh

Lời giải

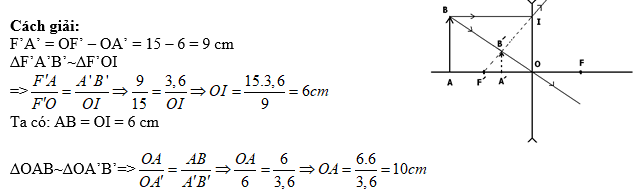
Bài tập 2

Đặt vật AB trước một thấu kính phân kì và vuông góc với trục chính của thấu kính thì cho ảnh lớn bằng một phần tư vật. Nếu đưa vật lại gần thấu kính thêm 5 cm thì thu được ảnh lớn bằng một phần ba vật. Tìm tiêu cự của thấu kính và khoảng cách ban đầu giữa vật và thấu kính đó.

Lời giải

Giả sử vị trí ban đầu của vật AB là d1, và ảnh tạo thành có độ lớn bằng một phần tư vật, nghĩa là d2 = 1/4d1.

– Ta có phương trình đầu tiên:

1/f = 1/d1 – 1/(1/4d1) = 1/d1 – 4/d1 = -3/d1

– Nếu đưa vật lại gần thấu kính thêm 5 cm, vị trí mới của vật là d1′ = d1 – 5 cm, và ảnh tạo thành có độ lớn bằng một phần ba vật, nghĩa là d2′ = 1/3d1′.

Ta có phương trình thứ hai: 1/f = 1/(d1 – 5) – 1/(1/3(d1 – 5) = 1/(d1 – 5) – 3/(d1 – 5) = -2/(d1 – 5)

Giờ ta có hệ phương trình với hai phương trình trên: -3/d1 = -2/(d1 – 5)

Để giải hệ phương trình này, chúng ta có thể nhân hai vế của phương trình thứ nhất với (d1 – 5) để loại bỏ mẫu số:

-3(d1 – 5) = -2d1

-3d1 + 15 = -2d1, d1 = 15 cm. Thay d1 = 15 cm vào phương trình đầu tiên:

1/f = -3/15 => f = -5 cm

Vậy tiêu cự của thấu kính là -5 cm (tiêu cự âm) và khoảng cách ban đầu giữa vật và thấu kính là d1 = 15 cm.

Lời kết

Trên đây là toàn bộ kiến thức về thấu kính phân kỳ? cách vẽ, công thức, bài tập áp dụng mà các em cần nắm bắt. Hãy nắm chắc lý thuyết và công thức cơ bạn trước khi làm bài tập để đạt hiệu quả cao. Chúc các em áp dụng hiệu quả và học tập tốt trong môn vật lý lớp 9!