Sự xác định đường tròn. Tính chất đối xứng của đường tròn
 23/11/2023 - admin
23/11/2023 - admin
Chương 2: Đường tròn là phần kiến thức trọng tâm trong bộ môn Toán 9 và đề thi tuyển sinh vào 10 THPT, vì vậy các em học sinh cần nắm rõ được phần kiến thức của chương này. Chương Đường tròn bắt đầu bằng bài đầu tiên là Sự xác định đường tròn và tính chất đối xứng của đường tròn. Với bài viết này đội ngũ THPT Lê Hồng Phong sẽ đồng hành cùng các em tìm hiểu bài học này với phần lý thuyết và các bài tập liên quan.
I. Lý thuyết
1. Định nghĩa về đường tròn
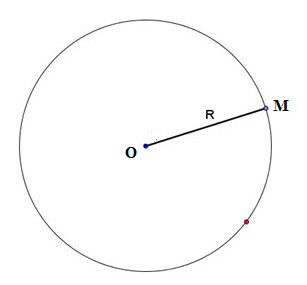
Đường tròn tâm O bán kính R > 0 là hình gồm các điểm cách điểm O một khoảng R kí hiệu là (O; R) hay (O).
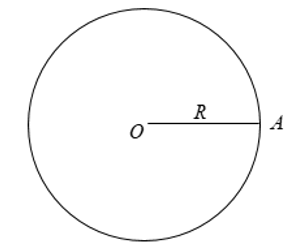
Nếu A nằm trên đường tròn (O; R) thì OA = R.
Nếu A nằm trong đường tròn (O; R) thì OA < R.
Nếu A nằm ngoài đường tròn (O; R) thì OA > R.
2. Cách xác định đường tròn
+ Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp tam giác vuông đó
+ Trong tam giác đều , tâm đường tròn ngoại tiếp là trọng tâm tam giác đó.
+ Trong tam giác thường:
Tâm đường tròn ngoại tiếp là giao điểm của 3 đường trung trực của 3 cạnh tam giác đó

Tâm đường tròn nội tiếp là giao điểm 3 đường phân giác trong của tam giác đó
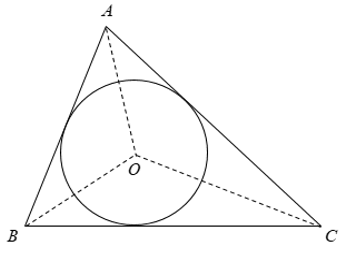
Chú ý: Không vẽ được đường tròn nào đi qua 3 điểm thẳng hàng
3. Tâm đối xứng
Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó.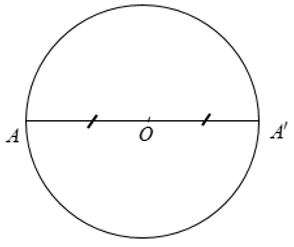 4. Trục đối xứng
4. Trục đối xứng
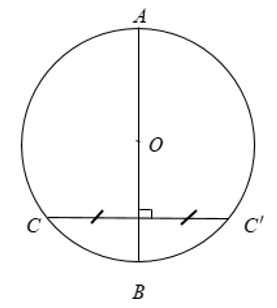
Đường tròn là hình có trục đối xứng. Bất kỳ đường kính nào của đường tròn cũng là trục đối xứng của đường tròn.
II. Bài tập minh họa SGK
Bài 1:
Cho hình chữ nhật ABCD có AB = 12cm, BC = 5cm. Chứng minh rằng bốn điểm A, B, C, D thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.
Lời giải:

Gọi O là giao điểm hai đường chéo của hình chữ nhật ABCD. Dựa vào tính chất của hình chữ nhật ta có:
OA = OB = OC = OD
Do đó, bốn điểm A, B, C, D cùng cách đều điểm O một khoảng bằng OA nên A, B, C, D cùng thuộc đường tròn tâm O bán kính R = OA
Xét tam giác ABC vuông tại B có:
AB = 12cm
BC = 5cm
Áp dụng định lí Py-ta-go ta có:
AC2 = AB2 + BC2
=> AC2 = 122 + 52 = 169
=> AC = ![]()
Ta lại có: ![]() (tính chất của đường chéo hình chữ nhật)
(tính chất của đường chéo hình chữ nhật)
Do đó, đường tròn đi qua bốn điểm A, B, C, D có tâm O và bán kính R = 6,5cm.
Bài 2:
Hãy nối mỗi ô ở cột trái với một ô ở cột phải để được khẳng định đúng:
| (1) Nếu tam giác có ba góc nhọn | (4) thì tâm của đường tròn ngoại tiếp tam giác đó nằm bên ngoài tam giác |
| (2) Nếu tam giác có góc vuông | (5) thì tâm của đường tròn ngoại tiếp tam giác đó nằm bên trong tam giác |
| (3) Nếu tam giác có góc tù | (6) thì tâm của đường tròn ngoại tiếp tam giác đó là trung điểm của cạnh lớn nhất |
| (7) thì tâm của đường tròn ngoại tiếp tam giác đó là trung điểm của cạnh nhỏ nhất |
Lời giải:
– Nối (1) với (5): Vì trong tam giác nhọn, giao của ba đường trung trực nằm bên trong tam giác nên tâm đường tròn ngoại tiếp nằm bên trong tam giác.
– Nối (2) với (6): Vì trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh đó. Tức là trung điểm cạnh huyền cách đều ba đỉnh của tam giác.
– Nối (3) với (4): Vì trong tam giác tù, giao của ba đường trung trực nằm bên ngoài tam giác nên tâm đường tròn ngoại tiếp nằm bên ngoài tam giác.
Bài 3 :
Chứng minh các định lí sau:
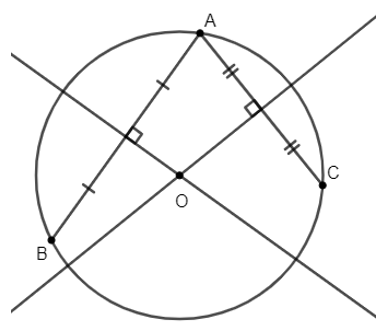
a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền
b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.
Lời giải:
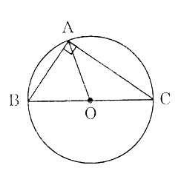
Hình a) + b)
a) Xét tam giác ABC vuông tại A. Gọi O là trung điểm của BC.
Ta có AO là đường trung tuyến ứng với cạnh huyền nên OA = OB = OC.
=> O là tâm của đường tròn đi qua A, B, C.
Vậy tâm của đường tròn ngoại tiếp ΔABC là trung điểm của cạnh huyền BC. (đpcm)
b) Xét tam giác ABC nội tiếp đường tròn (O) đường kính BC, ta có:
OA = OB = OC
Tam giác ABC có đường trung tuyến AO bằng nửa cạnh BC nên suy ra tam giác ABC vuông tại A. (đpcm)
Bài 4:
Lời giải:
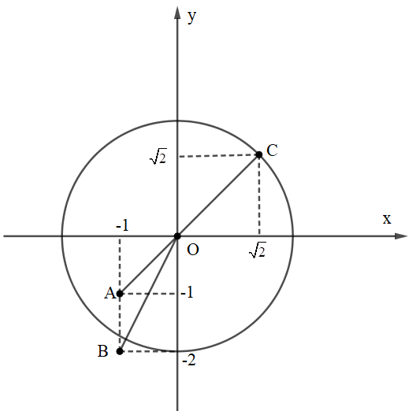

Bài 5:
Đố. Một tấm bìa hình tròn không còn dấu vết của tâm. Hãy tìm lại tâm của hình tròn đó.
Cách 1:
– Gấp tấm bìa sao cho hai phần của hình tròn trùng nhau, nếp gấp là một đường kính.
– Lại gấp như trên theo nếp gấp khác, ta được một đường kính thứ hai.
– Giao điểm của hai nếp gấp hay chính là giao hai đường kính và là tâm của đường tròn.
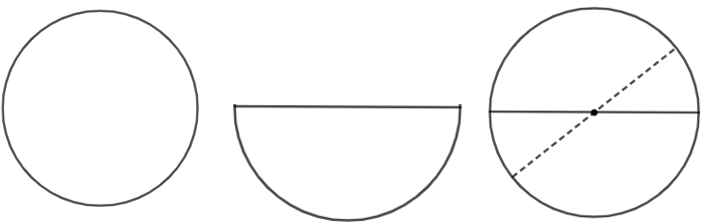
Cách 2:
– Lấy 3 điểm bất kì trên đường tròn. Vẽ hai dây AB và AC.
– Vẽ đường trung trực của AB và AC. Giao điểm O của đường trung trực này chính là tâm của hình tròn.