Cách tìm điều kiện xác định của phương trình và bất phương trình chuẩn

Kiến thức về phương trình và bất phương trình có lẽ đã không còn quá xa lạ gì với các bạn học sinh lớp 9 bởi đã được bắt đầu làm quen từ năm lớp 8. Đây là những kiến thức được coi là căn bản và rất quan trọng trong các kỳ thi đặc biệt là kỳ thi vào cấp 3. Để làm được dạng bài toán này, các em học sinh cần nắm được thế nào là tập xác định, điều kiện xác định của phương trình, bất phương trình.

Bài viết dưới đây, trường THPT Lê Hồng Phong sẽ chia sẻ với các em kiến thức cụ thể về dạng bài tìm điều kiện xác định của phương trình và bất phương trình, cùng xem ngay nhé!

Lý thuyết cơ bản về phương trình và bất phương trình

Trước khi đi vào bài tập, các em học sinh cần phải nắm vững những kiến thức cơ bản nhất như:

1. Khái niệm phương trình một ẩn

Cho hai hàm số như sau: y = f(x) và y = g(x) có tập xác định lần lượt sẽ là D1 và D2.

Đặt D = D1 ∩ D2. Mệnh đề chứa biến “f(x) = g(x)” được gọi là phương trình một ẩn, x gọi là ẩn và D gọi là tập xác định của phương trình.

Số x0 ∈ D gọi là một nghiệm của phương trình f(x) = g(x) nếu “f(x0) = g(x0)” là một mệnh đề đúng.

2. Phương trình tương đương

Hai phương trình được cho là hai phương trình tương đương khi và chỉ khi chúng có cùng chung một tập nghiệm. Nếu phương trình f1(x) = g1(x) tương đương với phương trình f2(x) = g2(x) thì ta sẽ viết như sau:

f1(x) = g1(x) ⇔ f2(x) = g2(x)

Định lý: Cho hai phương trình f(x) và g(x), cho f(x) = g(x) có tập xác định kí hiệu D và y = h(x) là một hàm số xác định trên tập D. Khi đó trên miền xác định D, phương trình đã cho sẽ tương đương với mỗi phương trình sau đây:

(1) f(x) + h(x) = g(x) + h(x)

(2) f(x).h(x) = g(x).h(x) với h(x) ≠ 0, ∀x ∈ D.

3. Phương trình hệ quả

Phương trình f1(x) = g1(x) có tập nghiệm kí hiệu là S1 được gọi là phương trình hệ quả của phương trình f2(x) = g2(x) có tập nghiệm kí hiệu là S2 nếu S1 ⊂ S2.

Khi đó viết: f1(x) = g1(x) ⇔ f2(x) = g2(x)

Định lý:

Khi bình phương cả hai vế của một phương trình, ta được phương trình hệ quả của phương trình đã cho như sau:  f(x) = g(x) ⇒ 2 = 2

Lưu ý:

– Nếu hai vế của một phương trình luôn luôn cùng dấu thì khi ta bình phương hai vế của nó, ta sẽ có được một phương trình tương đương.

– Nếu như phép biến đổi tương đương dẫn đến phương trình hệ quả, ta sẽ phải thử lại các nghiệm tìm được vào phương trình đã cho để phát hiện ra và loại bỏ đi những nghiệm ngoại lai.

4. Phương trình chứa ẩn ở mẫu

Phương trình chứa ẩn ở mẫu là phương trình có biểu thức chứa ẩn ở vị trí mẫu số.

Ví dụ:

2/(x + 3) = 0 là phương trình chứa ẩn ở mẫu (ẩn x)

2 – [4/(y² + 2y + 7)] = 0 là phương trình chứa ẩn ở mẫu (ẩn y)

Ta thấy, việc tìm điều kiện xác định là rất quan trọng trong việc tìm nghiệm của một phương trình. Sau đây, chúng tôi sẽ hướng dẫn phương pháp tìm điều kiện xác định của một phương trình.

5. Phương pháp tìm điều kiện xác định của phương trình

– Điều kiện xác định của phương trình là điều kiện các giá trị của ẩn trong phương trình f(0) được xác định.

Điều kiện xác định của phương trình viết tắt là ĐKXĐ.

– Điều kiện để biểu thức xác định là:

√f(0) xác định khi f(0) ≥ 0
1/f(0) xác định khi f(0) ≠ 0
1/√f(0) xác định khi f(0) > 0

Bài tập áp dụng tìm điều kiện xác định của phương trình và bất phương trình

Từ phần lý thuyết trên, các em hãy áp dụng và giải một số bài tập dưới đây nhé:

1. Trắc nghiệm

Câu 1: Tất cả các giá trị của ẩn x để biểu thức √(x – 3) có nghĩa là:

A) x < 3
B) x ≤ 3
C) x > 3
D) x ≥ 3

Đáp án chính xác là: D

Câu 2: Điều kiện xác định của biểu thức √(x – 8) là:

A) x ≥ 8
B) x > 8
C) x < 8
D) x ≤ 8

Đáp án chính xác là: A

Câu 3: Biểu thức √(2x – 8) có nghĩa khi và chỉ khi:

A) x ≤  -4
B) x ≤  4
C) x ≥ -4
D) x ≥ 4

Đáp án chính xác là: D

Câu 4: Với x > 0, thì biểu thức nào trong những biểu thức sau đây luôn có nghĩa?

A) √(2 – x)
B) √(x – 2)
C) √(2x)
D) √(-2x)

Đáp án chính xác là: C

Câu 5: Tất cả các giá trị của x để biểu thức √(-x² + 6x – 9) xác định là:

A) x = 6
B) x > 3
C) x = 3
D) x = -3

Đáp án chính xác là: C

Câu 6: Điều kiện xác định của biểu thức √[2017/(x – 2018)] là:

A) x ≥ 2018
B) x ≠ 2018
C) x > 2018
D) x < 2018

Đáp án chính xác là: C

Câu 7: Biểu thức √(1 – y²) xác định khi và chỉ khi:

A) y ≤ 1
B) y ≥ 1
C) -1 ≤ y ≤ 1
D) y ≠ 1

Đáp án chính xác là: C

Câu 8: Điều kiện của x để biểu thức √(3 – x) có nghĩa là:

A) x < 3
B) x ≤ 3
C) x > 3
D) x ≥ 3
Đáp án chính xác là: B

Câu 9: Điều kiện của x để biểu thức √(3x – 6) có nghĩa là:

A) x ≥ -1/2
B) x ≥ 2
C) x ≥ -2
D) x ≥ 1/2

Đáp án chính xác là: B

Câu 10: Tìm tất cả các giá trị của x để biểu thức P = √(x – 2) được xác định:

A) x < 2
B) x > 2
C) x ≥ 2
D) x ≤ 2

Đáp án chính xác là: C

Câu 11: Để biểu thức P(x) = √(2019 – 3x) + x – 2020 có nghĩa khi:

A) x ≥ 673
B) x ≠ 2020
C) x ≤ 673
D) x < 2019

Đáp án chính xác là: C

Câu 12: Điều kiện để biểu thức M = 1/(√x – 1) xác định là:

A) x > 1
B) x > 0
C) x > 0; x ≠ 1
D) x ≥; x ≠ 1

Đáp án chính xác là: D

2. Tự luận

Bài 1: Tìm các giá trị x thỏa mãn các điều kiện của mỗi bất phương trình sau đây:

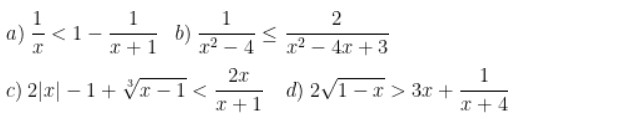
Hướng dẫn giải bài:

Bài 2: Chứng minh những bất phương trình sau đây là vô nghiệm:

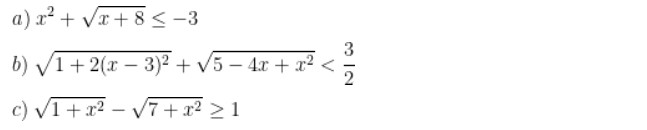
Hướng dẫn giải bài:

Bài 3: Em hãy giải thích vì sao các cặp bất phương trình sau đây là tương đương?

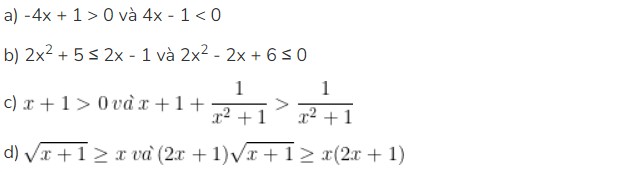
Hướng dẫn giải bài:

Một số câu hỏi khác về phương trình và bất phương trình

Điều kiện xác định của phương trình là gì?

Trả lời: Điều kiện xác định của phương trình là tập hợp các giá trị của biến mà khi thay vào phương trình, không gây ra các phép tính không xác định như chia cho 0 hoặc bất kỳ phép tính nào không có ý nghĩa.

Làm thế nào để xác định điều kiện xác định của một phương trình?

Trả lời: Để xác định điều kiện xác định, bạn cần tìm các giá trị của biến mà làm cho các phép tính trong phương trình có ý nghĩa, không gây ra việc chia cho 0 hoặc phép tính không xác định khác.

Tại sao điều kiện xác định quan trọng khi giải phương trình?

Trả lời: Điều kiện xác định quan trọng để đảm bảo rằng phương trình có nghiệm thực sự và tránh các tình huống không xác định hoặc vô lí trong quá trình giải phương trình.

Làm thế nào để áp dụng điều kiện xác định trong thực tế?

Trả lời: Để áp dụng điều kiện xác định trong thực tế, bạn cần hiểu rõ về các biểu thức và phép tính trong phương trình, xác định các giá trị của biến mà làm cho các phép tính không gây ra vấn đề, và từ đó giải phương trình một cách chính xác.

Lời kết

Trên đây, trường cấp 3 Lê Hồng Phong đã chia sẻ với bạn đọc những kiến thức rất cần thiết để có thể tìm được điều kiện xác định của phương trình và bất phương trình. Hy vọng bài viết sẽ giúp cho các em học sinh vẫn còn đang lơ mơ về phần kiến thức này có thể hiểu rõ hơn và làm bài tập một cách trơn tru, chính xác. Chúc các em học giỏi và đạt kết quả cao trong các kỳ thi.