26/01/2024 - admin
Toán 9 Bài 7: Vị trí tương đối của hai đường tròn
16/12/2023 - admin
Hai đường tròn có thể có các vị trí tương đối khác nhau tùy thuộc vào cách chúng được đặt trong không gian. Ngày hôm nay cùng THPT Lê hồng Phong tìm hiểu bài học này nhé. Nhằm giúp các em có thể nắm được kiến thức liên quan đến vị trí tương đối của hai đường tròn, bài viết này sẽ tổng hợp lại phần lý thuyết và bài tập minh họa cho bài học.
I. Lý thuyết vị trí tương đối của hai đường tròn
1. Ba vị trí tương đối của hai đường tròn.
a) Hai đường tròn cắt nhau.
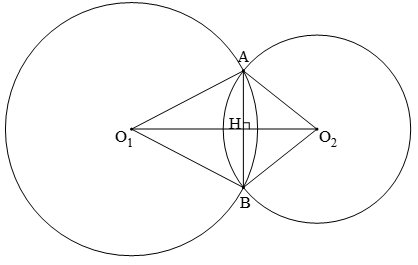
Hai đường tròn có hai điểm chung được gọi là hai đường tròn cắt nhau.
+ Hai điểm A, B là hai giao điểm.
+ Đoạn thẳng AB là dây chung.
+ Đặt O1A = R; O2A = r khi đó: |R – r| < O1O2 < R + r
+ Đường thẳng O1O2 là đường nối tâm, đoạn thẳng O1O2 là đoạn nối tâm.
+ Tính chất đường nối tâm: Đường nối tâm là đường trung trực của dây chung
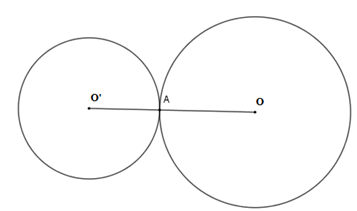
b) Hai đường tròn tiếp xúc nhau.
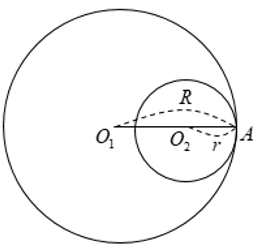
Hai đường tròn chỉ có một điểm chung được gọi là hai đường tròn tiếp xúc.
+ Điểm A gọi là tiếp điểm.
+ Có hai trường hợp tiếp xúc của hai đường tròn:
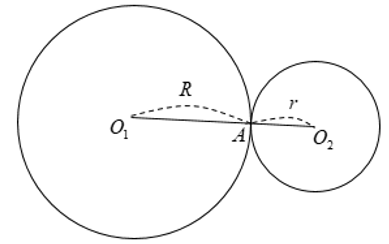
⋅ Tiếp xúc ngoài tại A: O1O2 = R + r
⋅ Tiếp xúc trong tại A: O1O2 = |R – r|
c) Hai đường tròn không giao nhau
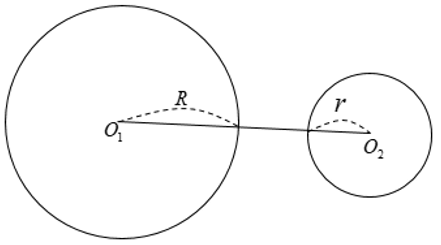
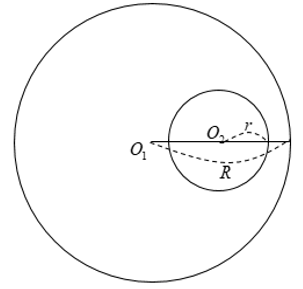
Hai đường tròn không có điểm chung nào được gọi là hai đường tròn không giao nhau.
+ Hai đường tròn ngoài nhau: O1O2 > R + r
+ Hai đường tròn đựng nhau: O1O2 < |R – r|
+ Đặc biệt, khi (O1) và (O2) đồng tâm: O1O2 = 0
2. Định lý
+ Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng nhau qua đường nối tâm, tức là đường nối tâm là đường trung trực của dây cung.
+ Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.
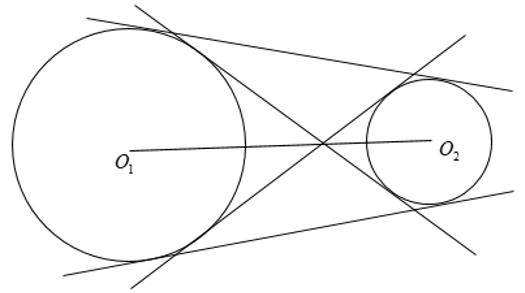
3. Tiếp tuyến chung của hai đường tròn
+ Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với cả hai đường tròn đó.
+ Tiếp tuyến chung ngoài không cắt đường nối tâm.
+ Tiếp tuyến chung trong cắt đường nối tâm.
II. Bài tập
Bài 33 – 119 SGK Toán 9 Tập 1:
Trên hình 89, hai đường tròn tiếp xúc nhau tại A. Chứng minh rằng OC // O’D.
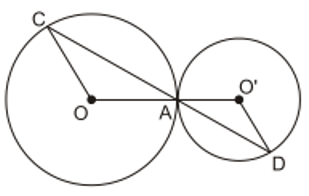
Lời giải:Ta có: OA = OC (bán kính) nên ΔOAC cân tại O.
Lại có O’A = O’D (bán kính) nên ΔO’AD cân tại O’
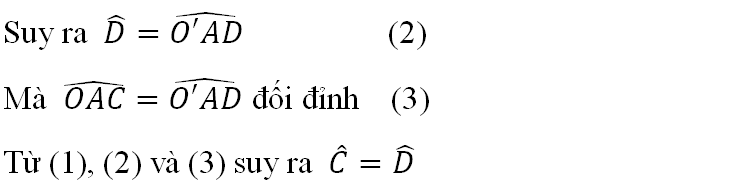
Vậy OC // O’D (có hai góc so le trong bằng nhau).
Bài 34 – 119 SGK Toán 9 Tập 1:
Cho hai đường tròn (O; 20cm) và (O’; 15cm) cắt nhau tại A và B. Tính đoạn nối tâm OO’, biết rằng AB = 24 cm. (Xét hai trường hợp: O và O’ nằm khác phía đối với AB; O và O’ nằm cùng phía đối với AB).
Lời giải:
– Trường hợp 1: O và O’ nằm khác phía đối với AB
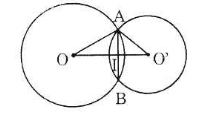
Gọi I là giao điểm của OO’ và AB. Theo tính chất đường nối tâm ta có:
AB ⊥ OO’ và AI = IB = 12
Áp dụng định lí Pitago, ta được:
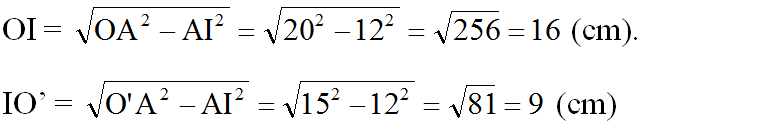
Vậy OO’ = OI + IO’ = 16 + 9 = 25 (cm)
– Trường hợp 2: O và O’ nằm cùng phía đối với AB
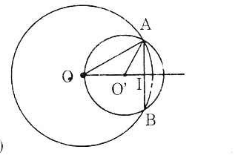
Tương tự như trường hợp 1, ta có:
Vậy OO’ = OI – O’I = 16 – 9 = 7 (cm).
Bài 35 – 122 SGK Toán 9 Tập 1:
Điền vào các ô trống trong bảng, biết rằng hai đường tròn (O; R) và (O’; r) có OO’ = d, R > r.
| Vị trí tương đối của hai đường tròn | Số điểm chung | Hệ thức giữa d, R, r |
|---|---|---|
| (O; R) đựng (O’; r) | ||
| d > R + r | ||
| Tiếp xúc ngoài | ||
| d = R – r | ||
| 2 |
Lời giải:
Ta có bảng sau:
| Vị trí tương đối của hai đường tròn | Số điểm chung | Hệ thức giữa d, R, r |
|---|---|---|
| (O; R) đựng (O’; r) | 0 | d < R – r |
| Ở ngoài nhau | 0 | d > R + r |
| Tiếp xúc ngoài | 1 | d = R + r |
| Tiếp xúc trong | 1 | d = R – r |
| Cắt nhau | 2 | R – r < d < R + r |
Bài 36 – 123 SGK Toán 9 Tập 1:
Cho đường tròn tâm O bán kính OA và đường tròn đường kính OA.
a) Hãy xác định vị trí tương đối của hai đường tròn.
b) Dây AD của đường tròn lớn cắt đường tròn nhỏ ở C. Chứng minh rằng AC = CD.
Lời giải:
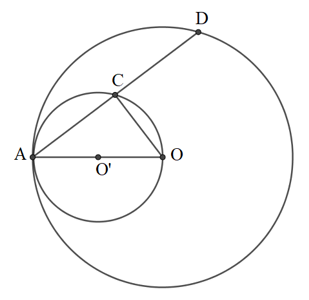
a)
Gọi O’ là tâm của đường tròn đường kính OA
Gọi R và r lần lượt là bán kính đường tròn tâm O và tâm O’.
Độ dài OO’ = d
Vì O’ là tâm của đường tròn đường kính OA nên r = O’A = O’O = 
Vì điểm O’ nằm giữa điểm O và A nên ta có:
AO’ + OO’ = OA
⇒ OO’ = OA – O’A hay d = R – r
Do đó, đường tròn (O’) tiếp xúc trong với đường tròn (O).
b)
Xét đường tròn (O’) có A, O, C cùng thuộc đường tròn và cạnh OA là đường kính của đường tròn (O’) nên tam giác CAO vuông tại C
=> OC ⊥ AD tại C
Xét đường tròn (O) có OC là một phần đường kính và AD là dây của đường tròn
Mà OC ⊥ AD tại C (chứng minh trên)
=> CA = CD (do đường kính vuông góc với một dây không đi qua tâm thì đi qua trung điểm dây đó).
Bài 37 – 123 SGK Toán 9 Tập 1:
Cho hai đường tròn đồng tâm O. Dây AB của đường tròn lớn cắt đường tròn nhỏ ở C và D. Chứng minh rằng AC = BD.
Lời giải:
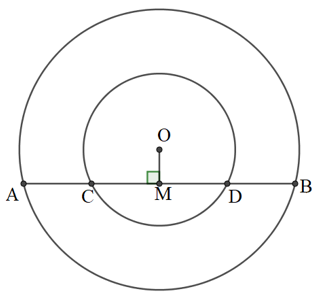
Giả sử vị trí các điểm theo thứ tự là A, C, D, B.
Vẽ OM ⊥ AB => OM ⊥ CD
Xét đường tròn (O; OC) (đường tròn nhỏ) có OM là một phần đường kính
CD là dây và OM ⊥ CD nên M là trung điểm của CD
⇒ MC = MD
Xét đường tròn (O; OA) (đường tròn lớn) có OM là một phần đường kính
AB là dây và OM ⊥ AB nên M là trung điểm của AB
⇒ MA = MB
Ta có: MA = MB, MC = MD
⇒ MA – MC = MB – MD
⇒ AC = BD.
(Trường hợp vị trí các điểm theo thứ tự là A, D, C, B chứng minh tương tự).
Tin khác
26/01/2024 - admin
Soạn bài Tiếng Anh 8 Unit 5 Communication (trang 54-55) – Global Success
26/01/2024 - admin
Soạn bài Tiếng Anh 8 Unit 5 A Closer Look 2 (trang 53-54) – Global Success
26/01/2024 - admin
Soạn bài Tiếng Anh 8 Unit 5 A Closer Look 1 (trang 52-53) – Global Success
24/01/2024 - admin
Soạn bài Tiếng Anh 8 Unit 5 Getting Started (trang 50-51) – Global Success
24/01/2024 - admin
Từ vựng Tiếng Anh 8 Unit 5: Our customs and traditions – Global Success
24/01/2024 - admin
Soạn bài Tiếng Anh 8 Unit 4 Project (trang 49) – Global Success
24/01/2024 - admin
