Toán 9 Bài 6: Tính chất của hai tiếp tuyến cắt nhau
 15/12/2023 - admin
15/12/2023 - admin
Tính chất của hai tiếp tuyến cắt nhau là một trong những phần kiến thức liên quan đến chủ đề Đường tròn. Nhằm giúp các em có thể nắm bắt được kiến thức bài học để phục vụ cho quá trình học, bài viết này của THPT Lê Hồng Phong sẽ bao gồm chi tiết vầ lý thuyết và phần bài tập có trong sách giáo khoa. Phần kiến thức này cùng sẽ phục vụ cho kỳ thi quan trọng tiếp theo của các bạn, vì vậy cùng theo dõi ngay sau đây nhé!
I. Lý thuyết tính chất của hai tiếp tuyến cắt nhau
1. Định lý về hai tiếp tuyến cắt nhau
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
+ Điểm đó cách đều hai tiếp điểm.
+ Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
+ Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm
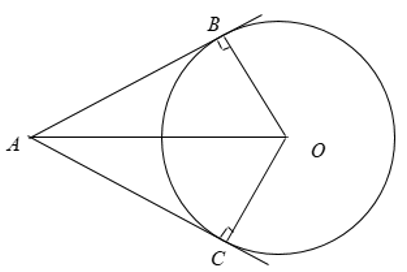
Ta có:![]()
2. Đường tròn nội tiếp của tam giác.
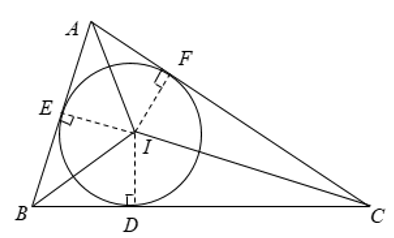
Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác, còn tam giác gọi là ngoại tiếp đường tròn, khi đó tam giác đó gọi là tam giác ngoại tiếp đường tròn.
Tâm của đường tròn nội tiếp tam giác là giao điểm của các đường phân giác các góc trong của tam giác
3. Đường tròn bàng tiếp tam giác.
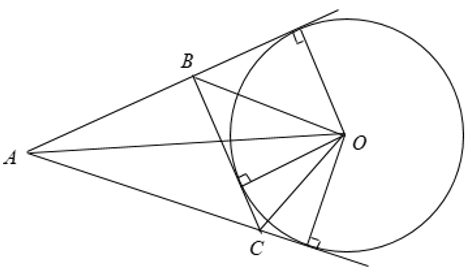
Đường tròn bàng tiếp tam giác là đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia.
Tâm của đường tròn bàng tiếp trong góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C, giao điểm này cùng nằm trên đường phân giác góc A.
Với một tam giác, có ba đường tròn bàng tiếp.
II. Bài tập sách giáo khoa
Bài 26 – 115 SGK Toán 9 Tập 1:
Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).
a) Chứng minh rằng OA vuông góc với BC.
b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO.
c) Tính độ dài các cạnh của tam giác ABC; biết OB = 2cm, OA = 4cm.
Lời giải:
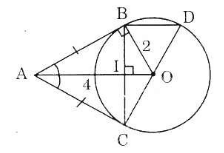
a) Ta có: AB = AC (tính chất của hai tiếp tuyến cắt nhau). Nên ΔABC cân tại A.
Lại có AO là tia phân giác của góc A nên AO ⊥ BC. (trong tam giác cân, đường phân giác cũng là đường cao)
b) Gọi I là giao điểm của AO và BC. Suy ra BI = IC (đường kính vuông góc với một dây).
Xét ΔCBD có :
CI = IB
CO = OD (bán kính)
⇒ BD//OI (OI là đường trung bình của tam giác BCD).
Vậy BD//AO.

Bài 27 – 115 SGK Toán 9 Tập 1:
Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn (O), nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và E. Chứng minh rằng chu vi tam giác ADE bằng 2AB.
Lời giải:
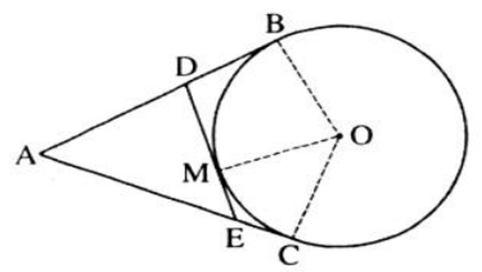
Theo tính chất hai tiếp tuyến cắt nhau ta có:
DM = DB, EM = EC, AB = AC
Chu vi ΔADE:
CΔADE = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB (đpcm)
Bài 28 – 116 SGK Toán 9 Tập 1:
Cho góc xAy khác góc bẹt. Tâm của các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên đường nào?
Lời giải:
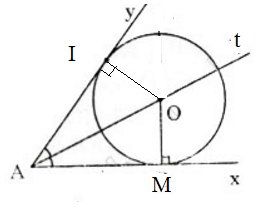
Gọi O là tâm của một đường tròn bất kì tiếp xúc với hai cạnh góc xAy. Theo tính chất của hai tiếp tuyến cắt nhau ta có:
![]()
Hay AO là tia phân giác của góc xAy.
Vậy tâm các đường tròn tiếp xúc với hai cạnh của góc xAy nằm trên tia phân giác của góc xAy.
Bài 29 – 116 SGK Toán 9 Tập 1:
Cho góc xAy khác góc bẹt, điểm B thuộc tia Ax. Hãy dựng đường tròn (O) tiếp xúc với Ax tại B và tiếp xúc với Ay.
Lời giải:
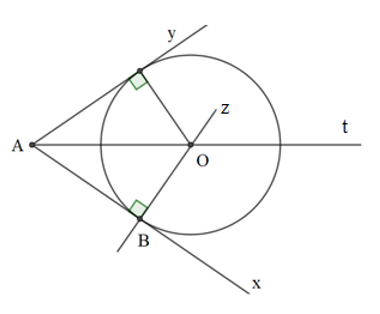
Đường tròn (O) tiếp xúc với hai tia Ax và Ay nên tâm O của (O) nằm trên tia phân giác của góc xAy. Do đó ta có cách dựng:
– Dựng tia phân giác At của góc xAy.
– Dựng đường thẳng Bz qua B và vuông góc với tia Ax.
– Giao điểm O của At và Bz là tâm của đường tròn cần dựng.
– Dựng đường tròn tâm O, bán kính R = OB, ta được đường tròn cần dựng.









