Toán 9 Bài 4: Vị trí tương đối của đường thẳng và đường tròn
 14/12/2023 - admin
14/12/2023 - admin
Bài toán vị trí tương đối giữa đường thẳng và đường tròn trong toán lớp 9 tập trung vào xác định mối quan hệ giữa đường thẳng và đường tròn trong mặt phẳng. Đây sẽ là phần kiến thức phục vụ nhiều cho các em trong quá trình học và chuẩn bị tốt nhất cho kỳ thi vào lớp 10. Nhằm giúp các em nắm được tổng quan bài học, THPT Lê Hồng Phong đã tổng hợp lại phần lý thuyết và bài tập có liên quan trong bài viết này. Cùng theo dõi ngay nhé!
I. Lý thuyết và vị trí tương đối của đường thẳng và đường tròn
1. Ba vị trí tương đối của đường thẳng và đường tròn
a) Đường thẳng và đường tròn cắt nhau
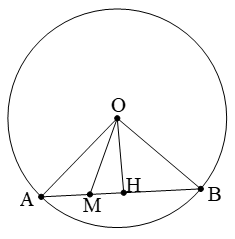
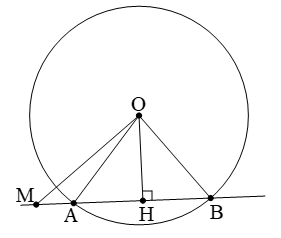
Khi một đường thẳng có hai điểm chung A, B với đường tròn (O) ta nói đường thẳng cắt đường tròn tại hai điểm phân biệt. Khi đó ta có những kết quả quan trọng sau:
![]()
Theo định lý Pitago ta có: OH2 = MO2 – MH2
Mặt khác ta cũng có: OH2 = R2 – AH2 nên suy ra
MO2 – MH2 = R2 – AH2 ⇔ MH2 – AH2 = MO2 – R2
⇔ (MH – AH)(MH + AH) = MO2 – R2
+ Nếu M nằm ngoài đoạn AB thì MA.MB = MO2 – R2
+ Nếu M nằm trong đoạn AB thì MA.MB = R2 – MO2
Mối liên hệ khoảng cách và dây cung: R2 = OH2 + AB2/4
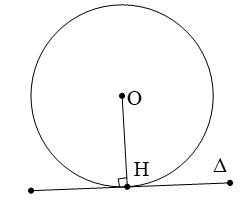
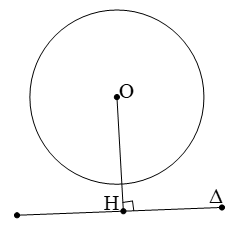
b) Đường thẳng và đường tròn tiếp xúc nhau.
Khi một đường thẳng Δ chỉ có một điểm chung H với đường tròn (O), ta nói đường thẳng tiếp xúc với đường tròn, hay Δ là tiếp tuyến của đường tròn (O). Điểm H gọi là tiếp điểm của tiếp tuyến với đường tròn (O)
Như vậy nếu Δ là tiếp tuyến của (O) thì Δ vuông góc với bán kính đi qua tiếp điểm
Ta có OH = R
c) Đường thẳng và đường tròn không giao nhau
Khi một đường thẳng Δ và đường tròn (O) không có điểm chung ta nói đường thẳng Δ và đường tròn (O) không giao nhau. Khi đó OH > R
2. Hệ thức giữa khoảng cách từ tâm đường tròn đến đường thẳng và bán kính của đường tròn
| Vị trí tương đối của đường thẳng và đường tròn | Số điểm chung | Hệ thức giữa d và R |
| Đường thẳng và đường tròn cắt nhau | 2 | d < R |
| Đường thẳng và đường tròn tiếp xúc nhau | 1 | d = R |
| Đường thẳng và đường tròn không giao nhau | 0 | d > R |
II. Bài tập sách giáo khoa
Bài 17 – 109 SGK Toán 9 Tập 1:
Điền vào các chỗ trống (…) trong bảng sau (R là bán kính của đường tròn, d là khoảng cách từ tâm đến đường thẳng):
| R | d | Vị trí tương đối của đường thẳng và đường tròn |
| 5cm | 3cm | … |
| 6cm | … | Tiếp xúc nhau… |
| 4cm | 7cm | … |
Lời giải:
Từ hệ thức giữa d và R ta có bảng:
| R | d | Vị trí tương đối của đường thẳng và đường tròn |
| 5cm | 3cm | Cắt nhau (d < R) |
| 6cm | 6cm | Tiếp xúc nhau (d = R) |
| 4cm | 7cm | Không giao nhau (d > R) |
Bài 18 – 110 SGK Toán 9 Tập 1:
Trên mặt phẳng tọa độ Oxy, cho điểm A(3; 4). Hãy xác định vị trí tương đối của đường tròn (A; 3) và các trục tọa độ.
Lời giải:
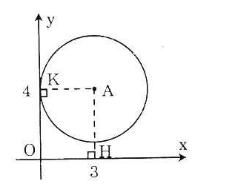
Kẻ AH ⊥ Ox, AK ⊥ Oy.
Vì AH = 4 > R = 3 nên đường tròn tâm (A) và trục hoành không giao nhau.
Vì AK = 3 = R nên đường tròn (A) và trục tung tiếp xúc nhau.
Bài 19 – 110 SGK Toán 9 Tập 1:
Cho đường thẳng xy. Tâm của các đường tròn có bán kính 1cm và tiếp xúc với đường thẳng xy nằm trên đường nào?
Lời giải:
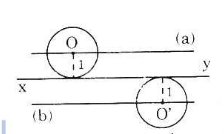
Gọi O là tâm của một đường tròn bất kì có bán kính bằng 1cm và tiếp xúc với đường thẳng xy.
Ta có: R = 1, và đường tròn tiếp xúc với đường thẳng xy nên ta có: d = R, suy ra d = 1.
=> Tâm O cách đường thẳng xy một khoảng cố định 1cm nên nằm trên các đường thẳng (a) và (b) song song với xy và cách xy một khoảng là 1cm.
Bài 20 – 110 SGK Toán 9 Tập 1:
Cho đường tròn tâm O bán kính 6cm và một điểm A cách O là 10cm. Kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Tính độ dài AB.
Lời giải:
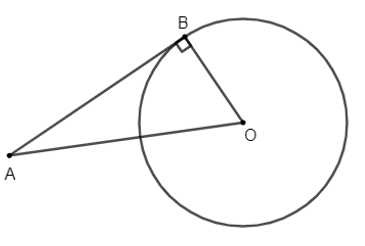
Xét đường tròn (O)










