Một số hệ thức về cạnh và góc trong tam giác vuông
 25/11/2023 - admin
25/11/2023 - admin
Các hệ thức về cạnh và góc trong tam giác vuông là phần kiến thức cơ bản của chương trình Toán hình học lớp 9, và đây cùng sẽ là phần kiến thức được sử dụng khá nhiều trong đề thi vào lớp 10 cũng như trong chương trình học THPT. Ngay bây giờ nếu em vẫn còn đang mơ hồ về kiến thức này thì hãy cùng THPT Lê Hồng Phong khám phá bài học này ngay nhé.
Lý thuyết cần nhớ
1. Các hệ thức trong tam giác vuông.
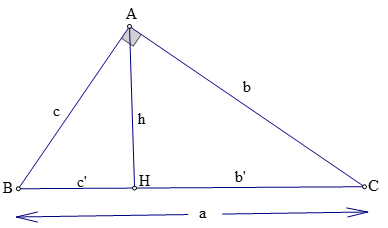
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
+ Cạnh huyền nhân với sin góc đối hay nhân với côsin góc kề.
+ Cạnh góc vuông kia nhân với tan của góc đối hay nhân với cotg của góc kề.
b = a.sinB = a.cosC; c = a.sinC = a.cosB; b = c.tgB = c.cotgC; c = b.tgC = b.cotgC.
Chú ý: Trong một tam giác vuông nếu cho trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và không kể góc vuông) thì ta sẽ tìm được các yếu tố còn lại.
2. Các dạng toán thường gặp
Dạng 1: Giải tam giác vuông
Phương pháp:
+ Giải tam giác là tính độ dài các cạnh và số đo các góc dựa vào dữ kiện cho trước của bài toán.
+ Trong tam giác vuông, ta dùng hệ thức giữa cạnh và các góc của một tam giác vuông để tính toán.
+ Các bài toán về giải tam giác vuông bao gồm :
Bài toán 1: Giải tam giác vuông khi biết độ dài một cạnh và số đo một góc nhọn.
Bài toán 2: Giải tam giác vuông khi biết độ dài hai cạnh.
Dạng 2: Tính cạnh và góc của tam giác
Phương pháp:
Bằng cách kẻ thêm đường cao ta làm xuất hiện tam giác vuông để áp dụng các hệ thức giữa cạnh và góc thích hợp.
II. Bài tập SGK
Bài 26 – 88 SGK Toán 9 Tập 1:
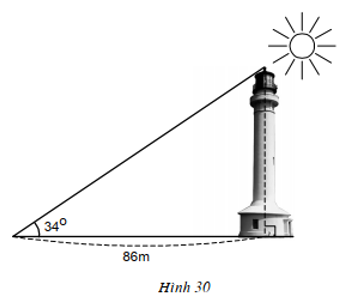
Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 34° và bóng của một tháp trên mặt đất dài 86m (h.30). Tính chiều cao của tháp (làm tròn đến mét).
Lời giải:
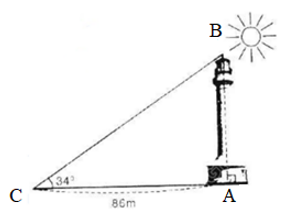
Ta kí hiệu các đỉnh như hình vẽ.
Xét tam giác ABC vuông tại A
Áp dụng hệ thức về cạnh và góc của tam giác vuông ta có:
AB = AC . tan C = 86 . tan34° ≈ 58 (m)
Vậy chiều cao của tháp là 58 m.
Bài 27 – 88 SGK Toán 9 Tập 1:
Giải tam giác ABC vuông tại A, biết rằng:
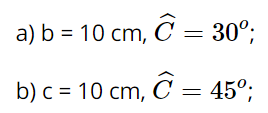

Lời giải:













