Lý thuyết đường thẳng song song và đường thẳng cắt nhau toán 9
 28/07/2023 - admin
28/07/2023 - admin
Đường thẳng song song và đường thẳng cắt nhau là một trong những phần kiến thức trọng tâm của toán lớp 9 mà học sinh cần lưu ý. Nhưng nếu muốn làm tốt phần bài tập này thì trước hết chúng ta cần nắm rõ Lý thuyết đường thẳng song song và đường thẳng cắt nhau.
Cùng THPT Lê Hồng Phong đi tìm hiểu bài học hôm nay nhé!

Lý thuyết đường thẳng song song và đường thẳng cắt nhau
1. Đường thẳng song song.
Hai đường thẳng y = ax + b (a ≠ 0) và y = a’x + b’ (a’ ≠ 0) song song với nhau khi và chỉ khi a = a’, b ≠ b’ và trùng nhau khi và chỉ khi a = a’, b = b’
Ví dụ: Đường thẳng y = 3x + 1 và đường thẳng y = 3x + 9 song song với nhau vì a = a’ = 3, b ≠ b’
2. Đường thẳng cắt nhau
Hai đường thẳng y = ax + b (a ≠ 0) và y = a’x + b’ (a’ ≠ 0) cắt nhau khi và chỉ khi a ≠ a’.
Ví dụ: Đường thẳng y = 4x +4 và đường thẳng y = 2x + 1 cắt nhau vì a ≠ a’
Các dạng bài tập thường gặp
1. Dạng 1
Chỉ ra vị trí tương đối của hai đường thẳng cho trước. Tìm tham số m để các đường thẳng thỏa mãn vị trí tương đối cho trước.
Phương pháp:
Cho hai đường thẳng ![]()
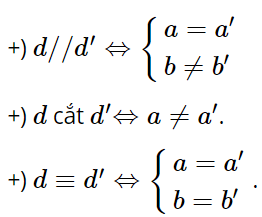
2. Dạng 2
Viết phương trình đường thẳng
Phương pháp:
+) Sử dụng vị trí tương đối của hai đường thẳng để xác định hệ số.
Ngoài ra ta còn sử dụng các kiến thức sau
+) Ta có y = ax + b với a ≠ 0, b ≠ là phương trình đường thẳng cắt trục tung tại điểm ![]() ,cắt trục hoành tại điểm
,cắt trục hoành tại điểm ![]()
+) Điểm ![]()
3. Dạng 3
Tìm điểm cố định mà đường thẳng d luôn đi qua với mọi tham số m
Phương pháp:
Gọi M (x;y) là điểm cần tìm khi đó tọa độ điểm M (x;y) thỏa mãn phương trình đường thẳng d.
Đưa phương trình đường thẳng d về phương trình bậc nhất ẩn m.
Từ đó để phương trình bậc nhất ax + b = 0 luôn đúng thì a = b =0.
Giải điều kiện ta tìm được x, y
Khi đó M (x;y) là điểm cố định cần tìm.
Lời kết
Trên đây là tổng hợp lý thuyết đường thẳng song song và đường thẳng cắt nhau. THPT Lê Hồng Phong rằng bài viết này sẽ giúp các em học tập hiệu quả và dễ dàng trong việc tiếp thu bài học hơn.









