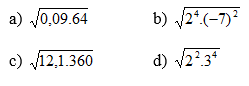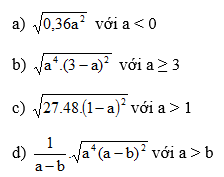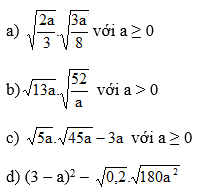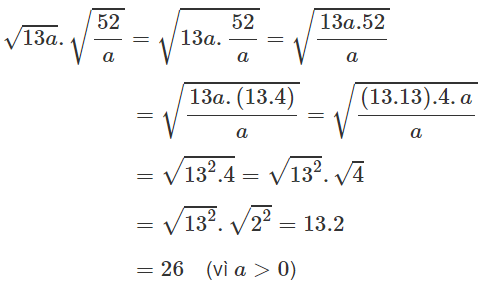Liên hệ giữa phép nhân và phép khai phương: công thức, bài tập

Để có thể làm tốt các bài tập liên quan đến chủ đề liên hệ giữa phép nhân và phép khai phương, chúng ta cần phải nắm được lý thuyết liên quan. Trong bài viết này, THPT Lê Hồng Phong sẽ giúp các em hệ thống lại các kiến thức cơ bản nhất được giới thiệu trong bài viết này. Bên cạnh đó là các dạng bài, quy tắc giải giúp các em làm bài tập tốt hơn.

Liên hệ giữa phép nhân và phép khai phương

Để có thể nắm chắc cách giải bài tập của phần này, đầu tiên chúng ta cùng tìm hiểu sâu hơn về lý thuyết bài học.

A. Lý thuyết Liên hệ giữa phép nhân và phép khai phương

1. Định lí

Với các số a và b không âm ta có: 

Lưu ý: 

+) Với hai biểu thức không âm A và B, ta cũng có:

+) Nếu không có điều kiện A và B không âm thì không thể viết đẳng thức trên.

Chẳng hạn được xác định nhưng đẳng thức  không xác định.

2. Áp dụng

a. Quy tắc khai phương một tích

Muốn khai phương một tích của những số không âm, ta có thể khai phương từng thừa số rồi nhân các kết quả với nhau.

+ Mở rộng: Với các số a, b, c không âm ta có:

b. Quy tắc nhân các căn bậc hai

Muốn nhân các căn bậc hai của những số không âm, ta có thể nhân các số dưới dấu căn với nhau rồi khai phương kết quả đó.

+ Mở rộng: Với các số a, b, c không âm ta có:

+ Với biểu thức A không âm, ta có: 

3. Dạng toán cơ bản

Dạng 1: Thực hiện phép tính

Sử dụng: Với hai biểu thức không âm A và B, ta có:

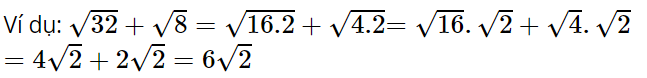
Sử dụng: Với hai biểu thức không âm A và B, ta có:

Ví dụ:

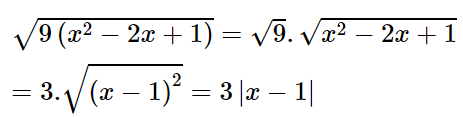
B. Giải bài tập SGK

Bài 17: Áp dụng quy tắc khai phương một tích, hãy tính:

Lời giải:

Bài 18: Áp dụng quy tắc nhân các căn bậc hai, hãy tính:

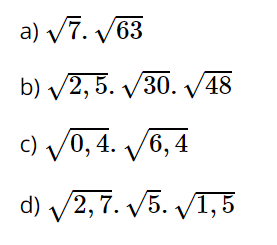
Lời giải:

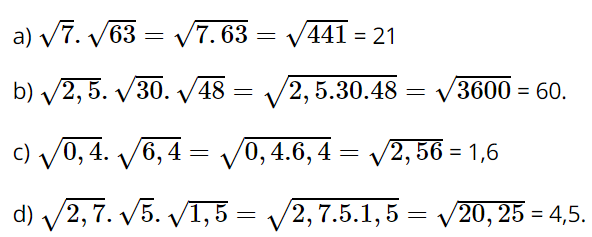
Bài 19: Rút gọn các biểu thức sau:

Lời giải:

Bài 20: Rút gọn các biểu thức sau:

Lời giải:

a) Ta có:

Bài 21: Khai phương tích 12.30.40 được:

(A) 1200 ;     (B) 120 ;     (C) 12 ;     (D) 240

Hãy chọn kết quả đúng.

Lời giải:

– Chọn B

– Vì ta có: