Hình nón, hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt
 23/12/2023 - admin
23/12/2023 - admin
Hình nón và hình nót cụt sẽ là 2 kiểu hình học tiếp theo mà các em được tìm hiểu trong chương này. Đây sẽ là phần kiến thức phục vụ nhiều cho các em trong quá trình học và chuẩn bị tốt nhất cho kỳ thi vào lớp 10. Nhằm giúp các em nắm được tổng quan bài học, THPT Lê Hồng Phong đã tổng hợp lại phần lý thuyết và bài tập có liên quan trong bài viết này. Cùng theo dõi ngay nhé!
I. Lý thuyết về Hình nón, hình nón cụt. Diện tích xung quanh và thể tích
Trước hết cùng tìm hiểu về lý thuyết của bài học nhé.
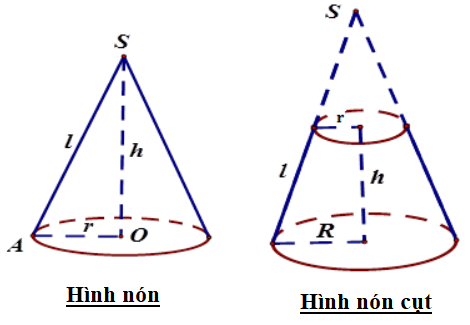
1. Hình nón
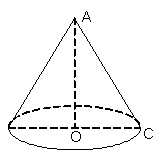
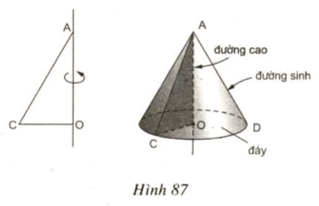
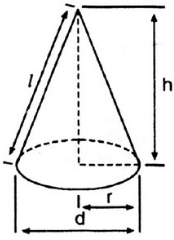
Khi quay tam giác vuông AOC một vòng quanh cạnh OA cố định thì được một hình nón.
+ Điểm A được gọi đỉnh của hình nón.
+ Hình tròn (O) được gọi là đáy của hình nón.
+ Mỗi vị trí của AC được gọi là một đường sinh của hình nón.
+ Đoạn AO được gọi là đường cao của hình nón.
2. Diện tích – thể tích của hình nón
Đặt AC = l; l là đường sinh
Cho hình nón có bán kính đáy R và đường sinh l, chiều cao h.
+ Diện tích xung quanh: Sxq = πRl
+ Diện tích toàn phần: Stp = πRl + πR2
+ Thể tích: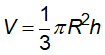
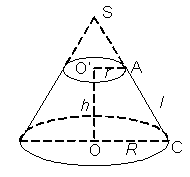
3. Hình nón cụt
Khi cắt hình nón bởi một mặt phẳng song song với đáy thì phần hình nón nằm giữa mặt phẳng nói trên và mặt phẳng đáy được gọi là một hình nón cụt.
+ Hai hình tròn (O) và (O’) được gọi là hai đáy.
+ Đoạn OO’ được gọi là trục. Độ dài OO’ là chiều cao.
+ Đoạn AC được gọi là đường sinh.
4. Diện tích – thể tích hình nón cụt
Cho hình nón cụt có các bán kính đáy R và r, chiều cao h, đường sinh l.
+ Diện tích xung qaunh: Sxq = π(R + r)l
+ Thể tích:![]()
II. Bài tập minh họa
Bài 15 – 117 SGK Toán 9 Tập 2:
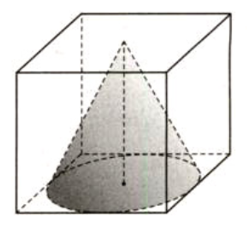
Một hình nón được đặt vào bên trong một hình lập phương như hình vẽ (cạnh của hình lập phương bằng 1) (h.93). Hãy tính:
a) Bán kính đáy của hình nón.
b) Độ dài đường sinh.
Lời giải
a) Ta có đường tròn đáy của hình nón nội tiếp trong hình vuông của một mặt của hình lập phương. Do đo bán kính của hình tròn đáy của hình nón bằng một nửa của cạnh hình lập phương và bằng 0,5.
b) Đỉnh của hình nón tiếp xúc với một mặt của hình lập phương nên đường cao của hình nón bằng với cạnh của hình lập phương và bằng 1.
Theo định lí Pitago, độ dài đường sinh của hình nón là:
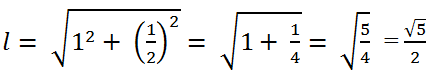
Bài 16 – 117 SGK Toán 9 Tập 2:
Cắt mặt cắt xung quanh của một hình nón theo một đường sinh và trải phẳng ra thành một hình quạt. Biết bán kính hình quạt tròn bằng độ dài đường sinh và độ dài cung bằng chu vi đáy.
Quan sát hình 94 và tính số đo cung của hình quạt tròn.
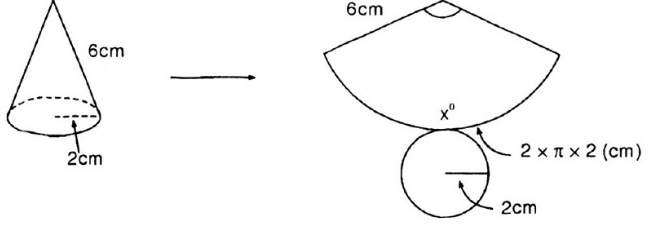
Lời giải

Bài 17 – 117 SGK Toán 9 Tập 2:
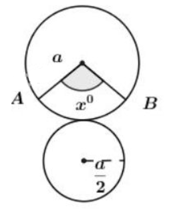
Khi quay tam giác vuông để tạo ra một hình nón như hình 87 thì góc CAO gọi là nửa góc ở đỉnh của hình nón. Biết nửa góc ở đỉnh của một hình nón là 30°, độ dài đường sinh là a. Tính số đo cung của hình quạt khi khai triển mặt xung quanh của hình nón.
Lời giải

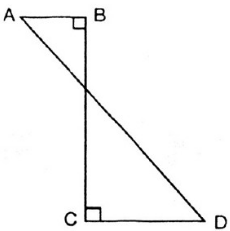
Bài 18 – 117 SGK Toán 9 Tập 2:
Hình ABCD (h.95) khi quay quanh BC thì tạo ra:
(A) Một hình trụ
(B) Một hình nón
(C) Một hình nón cụt
(D) Hai hình nón
(E) Hai hình trụ
Hãy chọn câu trả lời đúng.
Lời giải
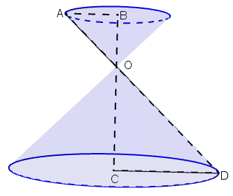
Nếu gọi O là giao điểm của BC và AD. Khi quay hình ABCD quanh BC thì có nghĩa là quay tam giác vuông OAB quanh OB và tam giác vuông OCD quanh OC. Mỗi hình quay sẽ tạo ra một hình nón. Vậy hình tạo ra sẽ là hai hình nón.
Vậy chọn D.
Bài 19 – 118 SGK Toán 9 Tập 2:
Hình khai triển của mặt xung quanh của một hình nón là một hình quạt. Nếu bán kính hình quạt là 16cm, số đo cung là 1200 thì độ dài đường sinh của hình nón là:
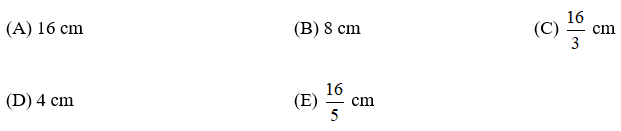
Lời giải
Khi khai triển mặt xung quanh của hình nón, ta được một hình quạt có bán kính bằng độ dài đường sinh.
Đề bài cho ta bán kính hình tròn chứa hình quạt là 16cm nên độ dài đường sinh của hình nón là 16cm.
Vậy chọn A.
Bài 20 – 118 SGK Toán 9 Tập 2:
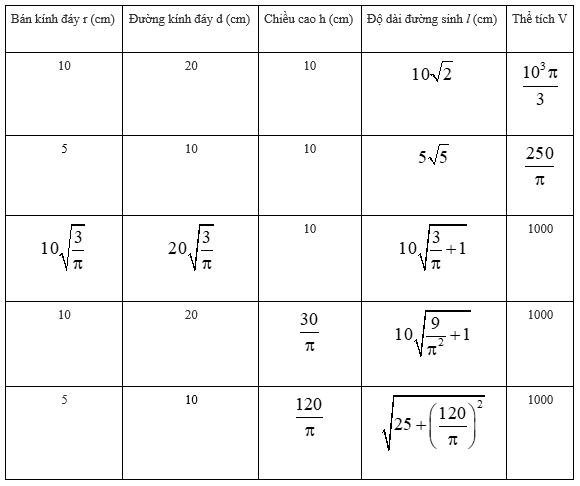
Hãy điền đủ vào các ô trống ở bảng sau (xem hình 96):
| Bán kính đáy r(cm) | Đường kính đáy d(cm) | Chiều cao h(cm) | Độ dài đường sinh l(cm) | Thể tích V |
| 10 | 10 | |||
| 10 | 10 | |||
| 10 | 1000 | |||
| 10 | 1000 | |||
| 1000 |
Lời giải
Cách tính:
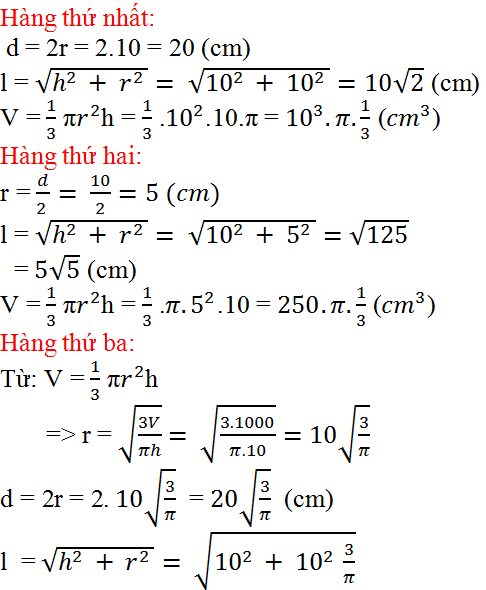

Bài 21 – 118 SGK Toán 9 Tập 2:
Cái mũ của chú hề với các kích thước cho theo hình vẽ (h.97). Hãy tính tổng diện tích vải cần có để làm nên cái mũ (không kể riềm, mép, phần thừa).
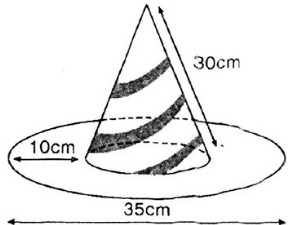
Lời giải

Bài 22 – 118 SGK Toán 9 Tập 2:
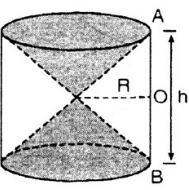
Hình 98 cho ta hình ảnh của một cái đồng hồ cát với các kích thước kèm theo (AO = OB).
Hãy so sánh tổng thể tích của hai hình nón và thể tích của hình trụ.
Lời giải










