Hình học Toán 9: Góc tạo bởi tia tiếp tuyến và dây cung
 20/12/2023 - admin
20/12/2023 - admin
Góc tạo bởi tia tiếp tuyến và dây cung là một trong những phần kiến thức liên quan đến chủ đề Đường tròn. Nhằm giúp các em có thể nắm bắt được kiến thức bài học để phục vụ cho quá trình học, bài viết này của THPT Lê Hồng Phong sẽ bao gồm chi tiết vầ lý thuyết và phần bài tập có trong sách giáo khoa. Phần kiến thức này cùng sẽ phục vụ cho kỳ thi quan trọng tiếp theo của các bạn, vì vậy cùng theo dõi ngay sau đây nhé!
I. Lý thuyết về góc tạo bởi tia tiếp tuyến và dây cung
1. Định nghĩa
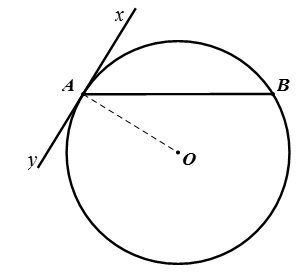
+ Góc tạo bởi tia tiếp tuyến và dây cung là góc có đỉnh nằm trên đường tròn, một cạnh là một tia tiếp tuyến còn cạnh kia chứa dây cung của đường tròn.
+ Cung nằm bên trong là cung bị chắn.
+ Hình vẽ:

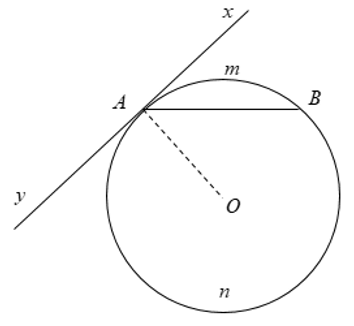
2. Định lý
Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.
Cụ thể:
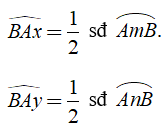
3. Hệ quả
+ Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.
+ Định lý bổ sung: Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn.
II. Bài tập minh họa
Bài 27 – 79 SGK Toán 9 Tập 2:
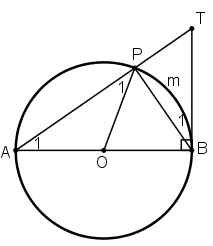
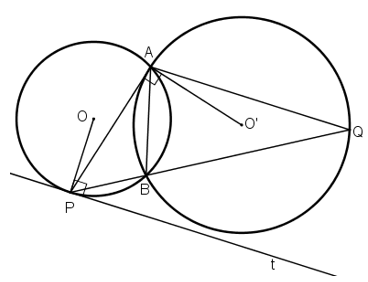
Cho đường tròn tâm O, đường kính AB. Lấy điểm P khác A và B trên đường tròn. Gọi T là giao điểm của AP với tiếp tuyến tại B của đường tròn. Chứng minh
![]()
Lời giải

Bài 28 – 79 SGK Toán 9 Tập 2:
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn (O’) cắt đường tròn (O) tại điểm thứ hai P. Tia PB cắt đường tròn (O’) tại Q. Chứng minh đường thẳng AQ song song với tiếp tuyến tại P của đường tròn (O).
Lời giải


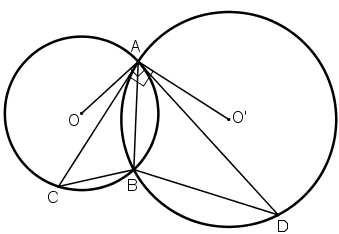
Bài 29 – 79 SGK Toán 9 Tập 2:
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Tiếp tuyến kẻ từ A đối với đường tròn (O’) cắt (O) tại C và đối với đường tròn (O) cắt (O’) tại D. Chứng minh ![]()
Lời giải
+ Trên đường tròn tâm O:
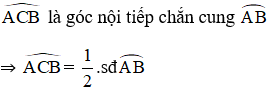
![]() là góc tạo bởi tiếp tuyến AD và dây AB
là góc tạo bởi tiếp tuyến AD và dây AB

+ Trên đường tròn tâm O’:
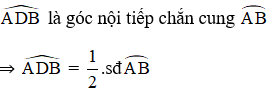
![]() là góc tạo bởi tiếp tuyến AC và dây AB
là góc tạo bởi tiếp tuyến AC và dây AB

Bài 30 – 79 SGK Toán 9 Tập 2:
Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung , cụ thể là: Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn(h.29).
Lời giải
Cách 1: Chứng minh trực tiếp
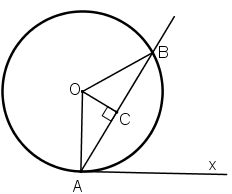
Gọi C là chân đường cao hạ từ O xuống AB.
ΔOAB có OA = OB = R nên tam giác này cân tại O
⇒ đường cao OC đồng thời là phân giác
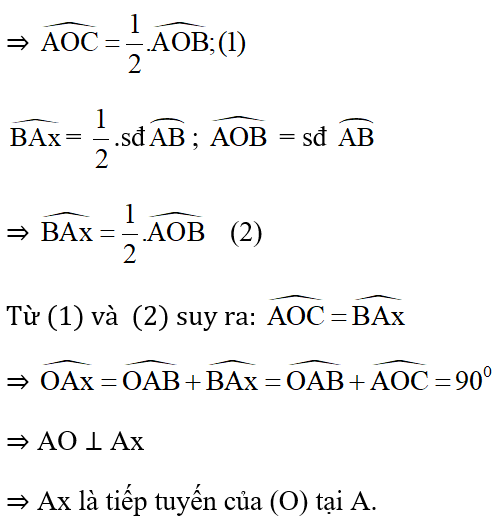
Cách 2: Chứng minh phản chứng
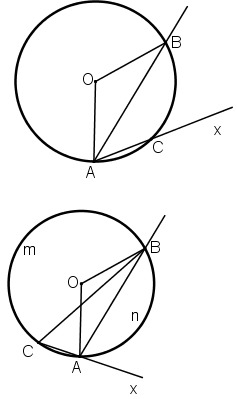
Giả sử Ax không phải tiếp tuyến của (O)
⇒ Ax là cắt (O) tại C khác A.
+ C nằm trên cung nhỏ AB

+ C nằm trên cung lớn AB
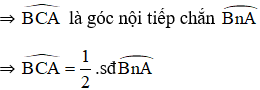
Mà ![]() là góc ngoài của tam giác BAC
là góc ngoài của tam giác BAC
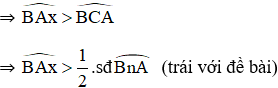
Vậy giả sử là sai ⇒ Ax là tiếp tuyến của đường tròn tâm O.