Hàm số bậc nhất là gì? Lý thuyết, cách giải, bài tập vận dụng

Hàm số bậc nhất là một trong những lý thuyết quan trọng và cơ bản nhất trong chương trình toán đại số. Nó cung cấp nền tảng cho nhiều kiến thức hàm số phức tạp hơn mà học sinh sẽ tiếp tục học trong chương trình toán trung học. Vậy hàm số bậc nhất là gì? Lý thuyết? Bài tập vận dụng? Ngày hôm nay cùng THPT Lê Hồng Phong đi tìm câu trả lời cho những câu hỏi trên nhé!

Hàm số bậc nhất là gì?

Dưới đây bao gồm tất cả những kiến thức xoay quanh hàm số bậc nhất

1. Khái niệm hàm số bậc nhất

Hàm số bậc nhất là hàm số có dạng: y = ax + b với a,b là các số cho trước và a ≠ 0

Khi b = 0 hàm số sẽ có dạng y = ax

2. Tính chất hàm số bậc nhất

Hàm số bậc nhất y = ax + b xác định với mọi x thuộc R, có tính chất như sau:

• Hàm số đồng biến trên R nếu a > 0
• Hàm số nghịch biến trên R nếu a < 0

Các dạng bài tập liên quan đến hàm số bậc nhất

Bài tập về hàm bậc nhất có 2 dạng cụ thể như sau:

Dạng 1: Xác định hàm số bậc nhất

Hàm số bậc nhất là hàm số có dạng y = ax + b (a≠0).

Ví dụ: Với điều kiện nào của m thì các hàm số nào sau đây là hàm số bậc nhất?

a) y = (m-1)x + m

b) y = (m2-2x -3)x2 + (m+1)x + m

c) y = √(m2-1).x + 2 .

Hướng dẫn giải:

a) y = (m-1)x + m là hàm số bậc nhất

y = (m-1)x + m ⇔ m – 1 ≠ 0 ⇔ m ≠ 1.

Vậy với mọi m ≠ 1 thì hàm số y = (m – 1)x + m là hàm số bậc nhất.

b) y = (m2-2x -3)x2 + (m+1)x + m là hàm số bậc nhất

y = (m2-2x -3)x2 + (m+1)x + m

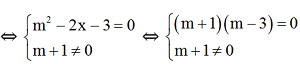
⇔ m – 3 = 0 ⇔ m = 3

Vậy với m = 3 thì hàm số y = (m2-2x -3)x2 + (m+1)x + m là hàm số bậc nhất là hàm số bậc nhất.

c) y = √(m2-1).x + 2 là hàm số bậc nhất

⇔ √(m2-1) ≠ 0 ⇔ m2 – 1 > 0 ⇔ m > 1 hoặc m < -1.

Vậy với m > 1 hoặc m < -1 thì hàm số y = √(m2-1).x + 2 là hàm số bậc nhất.

Dạng 2: Tìm m để hàm số đồng biến, nghịch biến

Ta có hàm số bậc nhất y = ax + b, (a≠0)

• Đồng biến trên R nếu a>0

• Nghịch biến trên R nếu a<0

Ví dụ: Tìm a để các hàm số dưới đây :

a) y = (a + 2)x + 3 đồng biến trên R.

b) y = (m2 – m).x + m nghịch biến trên R.

Hướng dẫn giải:

a) y = (a + 2)x + 3 đồng biến trên R

y = (a + 2)x + 3 ⇔ a + 2 > 0 ⇔ a > -2.

Vậy với mọi a > -2 thì hàm số y = (a + 2)x + 3 đồng biến trên R.

b) y = (m2 – m)x + m nghịch biến trên r

y = (m2 – m)x + m ⇔ m2 – m < 0 ⇔ m(m – 1) < 0 ⇔ 0 < m < 1.

Vậy với 0 < m < 1 thì hàm số y = (m2 – m)x + m nghịch biến trên R.

Lời kết

Trên đây là những kiến thức xoay quanh bài học về hàm số bậc nhất mà THPT Lê Hồng Phong tổng hợp lại được. Mong rằng những kiến thức này sẽ giúp ích cho các em trong quá trình học tập.