Đường kính và dây của đường tròn? Định nghĩa và bài tập liên quan
 07/12/2023 - admin
07/12/2023 - admin
Những kiến thức liên quan đến đường tròn là phần nội dung được coi là trọng tâm trong chương trình Toán lớp 9. Ngày hôm nay chúng ta sẽ cùng tìm hiểu một khía cạnh khác liên quan đến đường tròn là Đường kính và dây của đường tròn. Hãy cùng THPT Lê Hồng Phong tìm hiểu bài học này ngay sau đây nhé
Toán lớp 9 Đường kính và dây của đường tròn
Nhằm giúp các em nắm được kiến thức của bài giảng, đội ngũ Lê Hồng Phong đã chia bài viết này thành 2 nội dung chính là phần lý thuyết và bài tập sách giáo khoa.
I. Lý thuyết về đường kính và dây của đường tròn
1. So sánh độ dài của đường kính và dây.
Trong các dây của một đường tròn, dây lớn nhất là đường kính.
Ví dụ: Gọi AB là một dây bất kỳ của đường tròn (O; R). Chứng minh rằng AB ≤ 2R
+ Trường hợp 1: AB là đường kính
⇒ AB = 2R
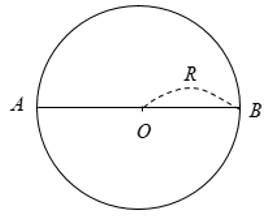
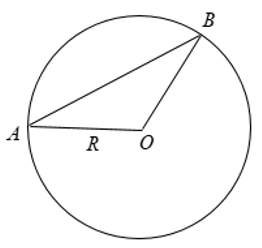
+ Trường hợp 2: AB không là đường kính
Xét tam giác AOB, áp dụng bất đẳng thức tam giác ta có:
AB < AO + OB = R + R = 2R
Vậy ta luôn có AB ≤ 2R
2. Quan hệ vuông góc giữa đường kính và dây.
+ Trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây đó.
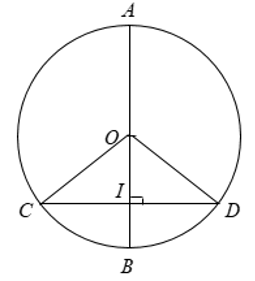
+ Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
3. Phương pháp giải bài tập liên quan
Tính độ dài đoạn thẳng và các yếu tố liên quan.
Ta thường sử dụng các kiến thức sau:
+) Quan hệ vuông góc giữa đường kính và dây
Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
+) Dùng định lý Pytago, hệ thức lượng trong tam giác vuông.
II. Bài tập minh họa
Câu hỏi 1 trang 103 SGK Toán 9:
Hãy đưa ra một ví dụ để chứng tỏ rằng đường kính đi qua trung điểm của một dây có thể không vuông góc với dây ấy.
Lời giải
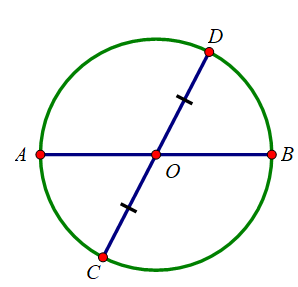
O là trung điểm của CD
AB đi qua trung điểm của CD nhưng AB không vuông góc với CD
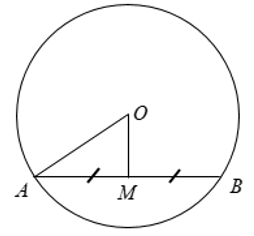
Câu hỏi 2 trang 103 SGK Toán 9:
Cho hình 67. Hãy tính độ dài dây AB, biết OA = 13 cm, AM = MB, OM = 5 cm.
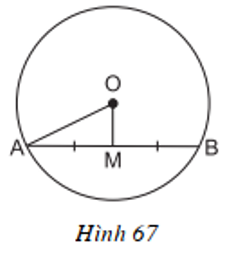
Lời giải
OM là 1 phần đường kính đi qua trung điểm của AB
⇒ OM ⊥ AB
Xét tam giác OAM vuông tại M có:
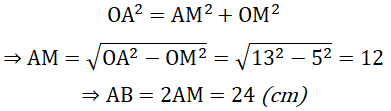
Bài 10 trang 104 SGK Toán 9:
Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng:
a) Bốn điểm B, E, D, C cùng thuộc một đường tròn.
b) DE < BC.
Lời giải:
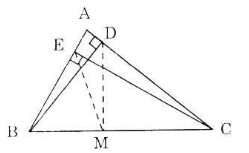
a) Gọi M là trung điểm của BC.

=> ME = MB = MC = MD
Do đó bốn điểm B, E, D, C cùng thuộc đường tròn tâm M. (đpcm)
b) Trong đường tròn tâm M nói trên, ta có DE là dây, BC là đường kính nên DE < BC.
Bài 11 trang 104 SGK Toán 9:
Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính AB, Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH = DK.
Gợi ý: Kẻ OM vuông góc với CD.
Lời giải:
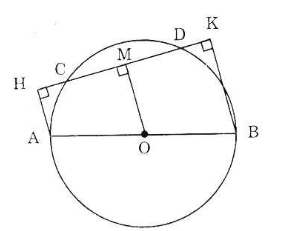
Kẻ OM ⊥ CD.
Vì AH // BK (cùng vuông góc HK) nên tứ giác AHKB là hình thang.
Hình thang AHKB có:
AO = OB (bán kính).
OM // AH // BK (cùng vuông góc HK)
=> OM là đường trung bình của hình thang.
=> MH = MK (1)
Vì OM ⊥ CD nên MC = MD (2)
Từ (1) và (2) suy ra CH = DK. (đpcm)









