Các khái niệm về hàm số bậc nhất toán 9: lý thuyết, bài tập VD
 29/07/2023 - admin
29/07/2023 - admin
Ở bài viết lần này THPT Lê Hồng Phong sẽ mang lại cho bạn bài kiến thức tổng hợp về hàm số bậc nhất và một số bài tập vận dụng toán 9 liên quan đến bài học. Đây sẽ là phần kiến thức nền tảng cho sau này, hãy chú trọng kiến thức này nhé.
Hàm số bậc nhất
Để giải được các bài toán về hàm số bậc nhất của toán 9, trước tiên các em cần nắm rõ định nghĩa và các công thức tính liên quan.
1. Lý thuyết hàm số bậc nhất
Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b. Trong đó a, b là các số cho trước và a≠0. Và khi b = 0 hàm số bậc nhất có dạng y = ax, biểu thị tương quan tỉ lệ thuận giữa y và x.
Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc R và có tính chất sau:
-
Đồng biến trên R nếu a>0
-
Nghịch biến trên R nếu a<0
2. Sự biến thiên của hàm số bậc nhất
Một kiến thức quan trọng khác mà các em cần quan tâm khi học bài tập này đó chính là sự biến thiên của hàm số bậc nhất. Lý thuyết và cách giải bài tập về sự biến thiên của hàm số bậc nhất cụ thể như sau:
Hàm số bậc nhất y = ax + b (a≠0) có tập xác định D = R, đồng biến trên R nếu a > 0 và nghịch biến trên R nếu a < 0.
Bảng biến thiên của hàm số bậc nhất:
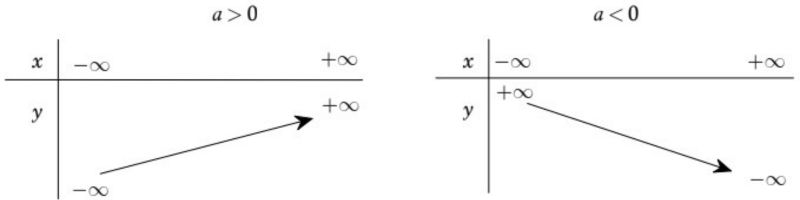
3. Các dạng bài tập cơ bản thường gặp
Bài tập về hàm bậc nhất có 2 dạng cụ thể như sau:
Dạng 1: Xác định hàm số bậc nhất
Hàm số bậc nhất là hàm số có dạng y = ax + b (a≠0).
Ví dụ: Với điều kiện nào của m thì các hàm số nào sau đây là hàm số bậc nhất?
a) y = (m-1)x + m
b) y = (m2-2x -3)x2 + (m+1)x + m
c) y = √(m2-1).x + 2 .
Hướng dẫn giải:
a) y = (m-1)x + m là hàm số bậc nhất
y = (m-1)x + m ⇔ m – 1 ≠ 0 ⇔ m ≠ 1.
Vậy với mọi m ≠ 1 thì hàm số y = (m – 1)x + m là hàm số bậc nhất.
b) y = (m2-2x -3)x2 + (m+1)x + m là hàm số bậc nhất
y = (m2-2x -3)x2 + (m+1)x + m
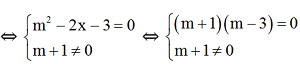
⇔ m – 3 = 0 ⇔ m = 3
Vậy với m = 3 thì hàm số y = (m2-2x -3)x2 + (m+1)x + m là hàm số bậc nhất là hàm số bậc nhất.
c) y = √(m2-1).x + 2 là hàm số bậc nhất
⇔ √(m2-1) ≠ 0 ⇔ m2 – 1 > 0 ⇔ m > 1 hoặc m < -1.
Vậy với m > 1 hoặc m < -1 thì hàm số y = √(m2-1).x + 2 là hàm số bậc nhất.
Dạng 2: Tìm m để hàm số đồng biến, nghịch biến
Ta có hàm số bậc nhất y = ax + b, (a≠0)
-
Đồng biến trên R nếu a>0
-
Nghịch biến trên R nếu a<0
Ví dụ: Tìm a để các hàm số dưới đây :
a) y = (a + 2)x + 3 đồng biến trên R.
b) y = (m2 – m).x + m nghịch biến trên R.
Hướng dẫn giải:
a) y = (a + 2)x + 3 đồng biến trên R
y = (a + 2)x + 3 ⇔ a + 2 > 0 ⇔ a > -2.
Vậy với mọi a > -2 thì hàm số y = (a + 2)x + 3 đồng biến trên R.
b) y = (m2 – m)x + m nghịch biến trên r
y = (m2 – m)x + m ⇔ m2 – m < 0 ⇔ m(m – 1) < 0 ⇔ 0 < m < 1.
Vậy với 0 < m < 1 thì hàm số y = (m2 – m)x + m nghịch biến trên R.
2. Đồ thị hàm số bậc nhất
Sau khi đã biết thế nào là hàm số bậc nhất thì các em cũng cần phải nắm rõ kiến thức về đồ thị hàm số bậc nhất. Như vậy mới có thể giải được các bài toán liên quan đến đồ thị hàm số bậc nhất.
1. Lý thuyết hàm số bậc nhất và đồ thị
Đồ thị của hàm số y = ax + b, (a≠0) là một đường thẳng cắt trục tung tại điểm có tung độ bằng b, song song với đường thẳng y = ax nếu b≠0 và trùng với đường thẳng y = ax nếu b=0.
Lưu ý rằng đồ thị của hàm số bậc nhất y = ax + b, (a≠0) còn được gọi là đường thẳng y = ax + b, b được gọi là tung độ gốc của đường thẳng.
2. Cách vẽ đồ thị hàm số bậc nhất
Trường hợp 1:
Khi b = 0 thì y = ax là đường thẳng đi qua gốc tọa độ O(0;0) và điểm A (1;a) đã biết.
Trường hợp 2: Xét y = ax với a khác 0 và b khác 0.
Ta đã biết đồ thị hàm số y = ax + b là một đường thẳng, do đó về nguyên tắc ta chỉ cần xác định được hai điểm phân biệt nào đó của đồ thị rồi vẽ đường thẳng qua hai điểm đó.
-
Cách 1:
-
Xác định hai điểm bất kỳ của đồ thị , chẳng hạn:
-
Cho x = 1 tính được y = a + b, ta có điểm A ( 1; a+b)
-
Cho x = -1 tính được y = -a + b, ta có điểm B (-1 ; -a + b)
-
-
Cách 2:
-
Xác định giao điểm của đồ thị với hai trục tọa độ:
-
Cho x = 0 tính được y = b, ta được điểm C (-b/a;0)
-
Cho y = 0 tính được x = -b/a, ta có điểm D (-b/a; 0)
-
Vẽ đường thẳng qua A, B hoặc C, D ta được đồ thị của hàm số y = ax + b
-
Dạng đồ thị của hàm số y = ax + b ( a≠0)
-
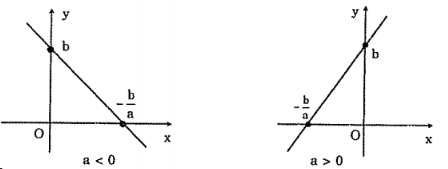
Trường hợp 3: Khi b khác 0
Ta cần xác định hai điểm phân biệt bất kì thuộc đồ thị.
Bước 1: Cho x = 0 => y = b. Ta được điểm P(0;b)∈Oy.
Cho y = 0 => x = −ba. Ta được Q(−ba;0)∈0x.
Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q, ta được đồ thị của hàm số y = ax + b.
Bài tập vận dụng của hàm số bậc nhất
Bài 1: Các hàm số sau đây có phải hàm số bậc nhất hay không? Nếu phải hãy chỉ ra hệ số a, b.
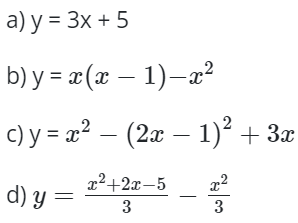
Bài 2: Tìm m để hàm số sau là hàm số bậc nhất
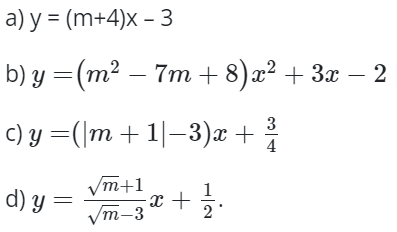
Bài 3: Tính giá trj hàm số
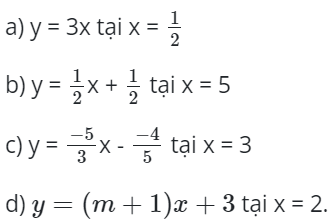
Bài 4: Tìm m để các giá trị hàm số sau thỏa mãn
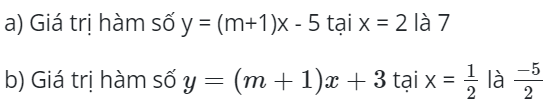
Bài 5: Tìm m để hàm số ![]()
Bài 6: Chứng minh hàm số sau luôn là hàm số bậc nhất
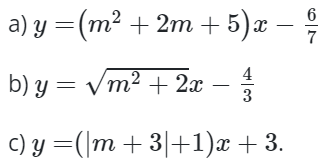
Bài 7: Các hàm số sau đồng biến hay nghịch biến
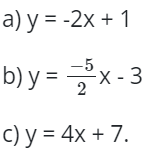
Bài 8: Tìm m để hàm số sau thỏa mãn

Bài 9: Chứng minh các hàm số sau:

Bài 10: Cho hàm số ![]()









