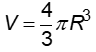Toán 9: Hình cầu. Diện tích mặt cầu và thể tích hình cầu
 28/12/2023 - admin
28/12/2023 - admin
Hình cầu là một loại hình học được tạo ra bởi việc xoay một vòng tròn quanh trục của nó. Ngày hôm nay chúng ta sẽ cùng tìm hiểu về hình cầu và diện tích mặt cầu, thể tích hình cầu. Nhằm giúp các em nắm được tổng quan bài học, THPT Lê Hồng Phong đã tổng hợp lại phần lý thuyết và bài tập có liên quan trong bài viết này. Cùng theo dõi ngay nhé!
I. Lý thuyết về hình cầu
1. Hình cầu.
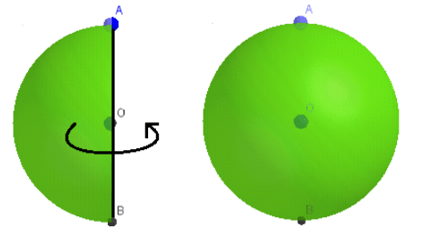
Khi quay nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định thì được một hình cầu.
+ Nửa đường tròn trong phép quay nói trên tạo thành một mặt cầu.
+ Điểm O được gọi tâm, R là bán kính của hình cầu hay mặt cầu đó.
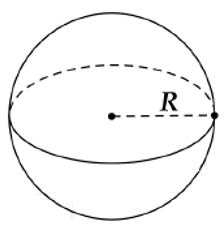
2. Cắt hình cầu bởi một mặt phẳng
Khi cắt hình cầu bởi một mặt phẳng ta được một hình tròn.
Khi cắt mặt cầu bán kính R bởi một mặt phẳng ta được một đường tròn:
+ Đường tròn đó có bán kính R nếu mặt phẳng đi qua tâm (gọi là đường tròn lớn).
+ Đường tròn đó có bán kính bé hơn R nếu mặt phẳng không đi qua tâm.

3. Diện tích – thể tích của hình cầu
Cho hình cầu bán kính R.
+ Diện tích mặt cầu: S = 4πR2
+ Thể tích hình cầu:
II. Bài tập minh họa
Bài 30 – 124 SGK Toán 9 Tập 2:
Nếu thể tích của một hình cầu là ![]() thì trong các kết quả sau đây, kết quả nào là bán kính của nó,
thì trong các kết quả sau đây, kết quả nào là bán kính của nó, ![]() ?
?
(A) 2cm; (B) 3cm; (C) 5cm; (D) 6cm; (E) Một kết quả khác.
Lời giải

Bài 31 – 124 SGK Toán 9 Tập 2:
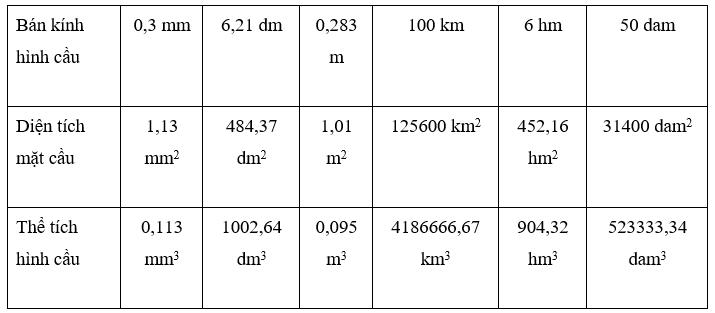
Hãy điền vào các ô trống ở bảng sau:
| Bán kính hình cầu | 0,3mm | 6,21dm | 0,283m | 100km | 6hm | 50dam |
| Diện tích mặt cầu | ||||||
| Thể tích hình cầu |
Lời giải
Cách tính:
Dòng thứ nhất : S = 4πR2 . Thay số vào ta được
R = 0,3 mm ⇒ S = 4.3,14. 0,32 = 1,13 (mm2)
R = 6,21 dm ⇒ S = 4.3,14. 6,212 = 484,37 (dm2)
R = 0,283 m ⇒ S = 4.3,14. 0,2832 = 1,01 (m2)
R = 100 km ⇒ S = 4.3,14. 1002 = 125600 (km2)
R = 6 hm ⇒ S = 4.3,14. 62 = 452,16 (hm2)
R = 50 dam ⇒ S = 4.3,14. 502 = 31400 (dam2)

Bài 32 – 125 SGK Toán 9 Tập 2:
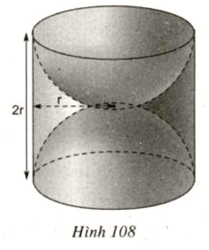
Một khối gỗ dạng hình trụ, bán kính đường tròn đáy là r, chiều cao 2r (đơn vị :cm). Người ta khoét rỗng hai nửa hình cầu như hình 108. Hãy tính diện tích bề mặt của khối gỗ còn lại (diện tích cả ngoài lẫn trong).
Lời giải
Diện tích phần cần tính gồm diện tích xung quanh của một hình trụ bán kính đường tròn đáy r (cm), chiều cao là 2r (cm) và một mặt cầu bán kính r (cm).
Diện tích xung quanh của hình trụ:
Sxq = 2πrh = 2πr.2r = 4πr2 (cm2)
Diện tích mặt cầu:
S = 4πr2 (cm2)
Diện tích cần tính là:
4πr2 + 4πr2 = 8πr2 (cm2)
Bài 33 – 125 SGK Toán 9 Tập 2:
Dụng cụ thể thao.
Các loại bóng cho trong bảng đều có dạng hình cầu. Hãy điền vào các ô trống ở bảng sau(làm tròn kết quả đến chữ số thập phân thứ hai):
| Loại bóng | Quả bóng gôn | Quả khúc côn cầu | Quả ten-nit | Quả bóng bàn | Quả bi-a |
| Đường kính | 42,7mm | 6,5cm | 40mm | 61mm | |
| Độ dài đường tròn lớn | 23cm | ||||
| Diện tích | |||||
| Thể tích |
Lời giải
| Loại bóng | Quả bóng gôn | Quả khúc côn cầu | Quả ten-nit | Quả bóng bàn | Quả bi-a |
| Đường kính | 42,7mm | 7,32cm | 6,5cm | 40mm | 61mm |
| Độ dài đường tròn lớn | 134,08mm | 23cm | 20,41cm | 125,6mm | 191,54mm |
| Diện tích | 57,25cm2 | 168,25cm2 | 132,67cm2 | 5024mm2 | 11683,94mm2 |
| Thể tích | 40,74cm3 | 205,26cm3 | 143,72cm3 | 33,49 cm3 | 118,79cm3 |
Cách tính:



Bài 34 – 125 SGK Toán 9 Tập 2:
Khinh khí cầu của nhà Mông-gôn-fi-ê (Montgolfier)
Lời giải
Diện tích mặt khinh khí cầu là:
S= πd2=3,14.112=379,94 ( m2)