Kiến Thức Trọng Tâm Và Cấu Trúc Đề Thi Vào 10 Môn Toán 2024

Kì thi vào lớp 10 được xem là bước ngoặt lớn đầu tiên trên chặng đường học tập của các em. Ở giai đoạn này, tâm lý của các em khá lo lắng do lượng kiến thức quá nhiều và sách tham khảo thì đa dạng, học sách nào mới đúng trọng tâm. Cùng trường THPT Lê Hồng Phong tìm hiểu kiến thức trọng tâm và cấu trúc đề thi vào 10 môn Toán 2024 nhé!

1. Kiến thức cần nhớ môn Toán chuyên đề Đại số

Dựa vào cấu trúc đề thi môn Toán của những năm trước, có thể thấy kiến thức trong đề giống nhau đến 70-80%. Từ kinh nghiệm đó kèm hướng dẫn từ thầy cô, các bạn học sinh có thể xác định những nhóm kiến thức trọng tâm cần tập trung ôn luyện ở chuyên đề Đại số.

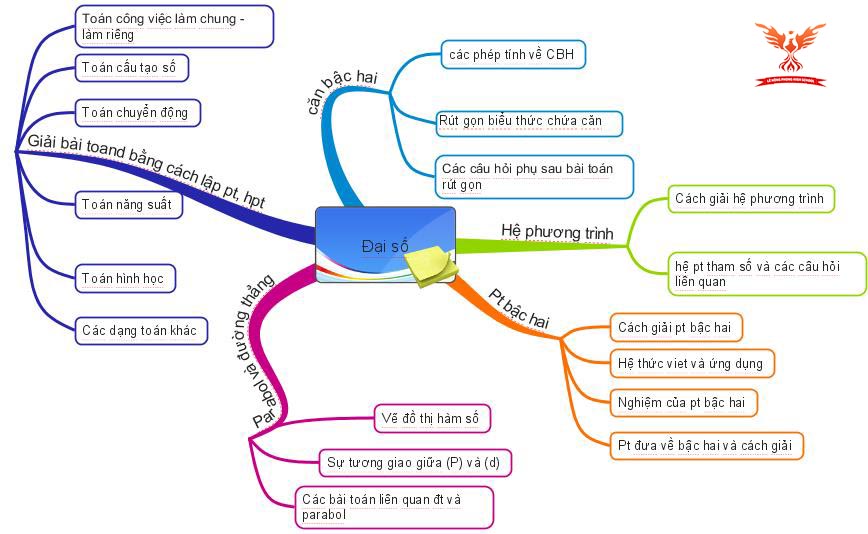
1.1. Rút gọn và tính giá trị biểu thức

Để làm câu hỏi rút gọn và tính giá trị biểu thức, các bạn cần nắm chắc định nghĩa về căn bậc hai, các quy tắc biến đổi căn thức, tính chất của phân số, 7 hằng đẳng thức đáng nhớ và vận dụng phương pháp phân tích đa thức thành nhân tử và rút gọn biển thức.

Với biểu thức số học, các bạn cần tiến hành 2 bước cơ bản để rút gọn biểu thức:

• Tim nhân tử chung bằng cách phân tích tử và mẫu
• Rút gọn nhân tử chung.

Với biểu thức đại số, các bạn thực hiện các bước sau để rút gọn:

• Phân tích tử và mẫu thành nhân tử
• Tìm điều kiện xác định
• Rút gọn từng phân thức
• Thực hiện các phép biến đổi đồng chất như:

• Quy đồng
• Bỏ ngoặc bằng cách nhân đơn, đa thức hoặc dùng hằng đẳng thức.
• Thu gọn các hạng tử đồng dạng.
• Phân tích thành nhân tử – rút gọn.

1.2. Phương trình và hệ phương trình

Để giải phương trình và hệ phương trình, các bạn cần ôn kỹ kiến thức về hệ phương trình bậc nhất 2 ẩn, phương trình bậc hai, phương trình, hệ phương trình đưa về phương trình bậc hai, định lý Viét, giải bài toán bằng cách lập phương trình, hệ phương trình.

Các dạng bài thuộc chuyên đề phương trình và hệ phương trình đều đều xoay quanh kiến thức cần ôn, cụ thể:

• Giải hệ phương trình bậc nhất hai ẩn có nghiệm duy nhất.
• Giải các dạng toán vận dụng định lý Viet.
• Tìm nghiệm của phương trình bậc hai theo công thức.
• Giải bài toán bằng cách lập phương trình (hoặc hệ phương trình), đưa về phương trình bậc hai một ẩn hoặc hệ phương trình bậc nhất 2 ẩn.

1.3. Hàm số và đồ thị

Các bạn cần ôn tập kiến thức về hàm số y = ax + b và hàm số y =  cx2. Phần kiến thức yêu cầu kĩ năng nhận biết và vẽ đồ thị hàm số bậc nhất, hàm số bậc hai, xác định các yếu tố có liên quan đến tính chất và đồ thị hai hàm số trên.

Đề thi môn Toán vào lớp 10 thường ra các câu hỏi dạng:

• Vẽ đồ thị hàm số với a, b, c là số nguyên.
• Lập phương trình đường thẳng theo các điều kiện cho trước.
• Xác định giao điểm đồ thị hai hàm số bằng giải phương trình bậc hai đơn giản (có 1 nghiệm nguyên).

1.4. Lập phương trình

Lập phương trình là kiến thức cơ bản rất quan trọng trong chương trình môn Toán lớp 9 vì được áp dụng vào nhiều dạng bài tập về chuyển động, hình học, xác suất, vật lý, hoá học, bài toán thực tế.

Để giải bài toán yêu cầu lập phương trình, các bạn cần ghi nhớ các bước sau:

• Chọn ẩn và đặt điều kiện cho ẩn.
• Biểu diễn các đại lượng chưa biết theo ẩn.
• Lập phương trình dựa vào các dữ kiện đã có.
• Giải phương trình
• Chọn các nghiệm thỏa mãn điều kiện của ẩn và kết luận.

2. Kiến thức cần nhớ môn Toán chuyên đề Hình học

Nếu muốn đạt được kiểm khá giỏi trong bài thi môn Toán vào lớp 10, các em học sinh phải làm được câu hỏi Toán hình. Dưới đây là hệ thống kiến thức quan trọng kèm những dạng bài thường xuất hiện, được chọn lọc từ đề thi của các tỉnh, thành phố trên cả nước các năm trước.

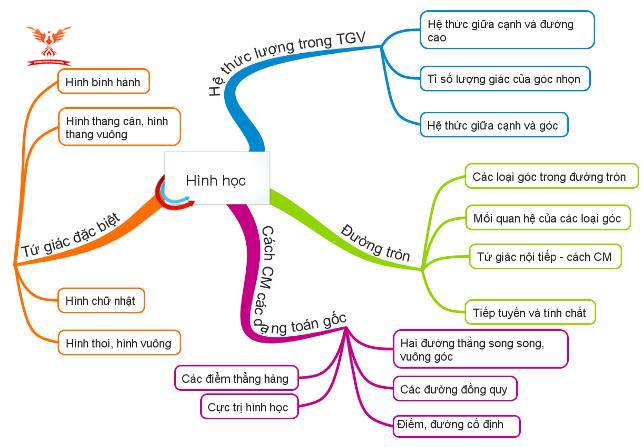
2.1. Lý thuyết quan trọng cần nhớ

Với chuyên đề Hình học, các bạn học sinh cần học thuộc các định lí hệ thức lượng trong tam giác vuông, định nghĩa tỉ số lượng giác của góc nhọn, hệ thức về cạnh và góc trong tam giác vuông, góc và đường tròn.

• Hệ thức lượng trong tam giác vuông

• Hệ thức lượng cho tam giác ABC vuông tại A, đường cao AH:
  • b² = ab’ ; c² = ac’
  • h² = b’c’
  • ah = bc
  • b² + c² = a² (Định lí Pytago)
  • 1/h² = 1/b² +1/c²
• Tỉ số lượng giác của góc nhọn trong tam giác vuông ABC, góc nhọn α (0°< α <90°):

• Hệ thức về cạnh và góc trong tam giác vuông: Trong một tam giác vuông, mỗi cạnh góc vuông bằngCạnh huyền nhân với sin góc đối hoặc nhân với cos góc kề.

• Hệ thức về cạnh và góc trong tam giác vuông: Trong một tam giác vuông, mỗi cạnh góc vuông bằng:

• • Cạnh huyền nhân với sin góc đối hoặc nhân với cos góc kề.
  • Cạnh góc vuông kia nhân với tan góc đối hoặc nhân với cot góc kề.

• Góc và đường tròn

Kiến thức về góc và đường tròn cần học xoay quanh quan hệ vuông góc giữa đường kính cà dây, liên hệ giữa đường kính và dây cung, dây cung và khoảng cách đến tâm, tính chất và các dấu hiệu nhận biết tiếp tuyến của đường tròn, các góc nội tiếp và cung chắn, các tính độ dài đường tròn, cung tròn, diện tích hình tròn và diện tích hình quạt tròn.

2.2. Dạng bài thường gặp cần nhớ

Dưới đây là những dạng bài tập quen thuộc mà các bạn học sinh dễ gặp trong đề thi Toán vào lớp 10.

2.2.1. Tứ giác nội tiếp

Tứ giác nội tiếp nội tiếp đường tròn là tứ giác có 4 điểm nằm trên một đường tròn.

Cách giải bài toán về tứ giác nội tiếp như sau:

• Chứng minh 4 đỉnh của tứ giác cùng nằm trên một đường tròn.
• Chứng minh tứ giác có tổng hai góc đối diện bất kì bằng 180 độ.
• Chứng minh tứ giác có hai đỉnh kề nhau nhìn cạnh đối diện dưới cùng một góc.
• Chứng minh 4 đỉnh của tứ giác cách đều tâm, khoảng cách bằng bán kính đường tròn.

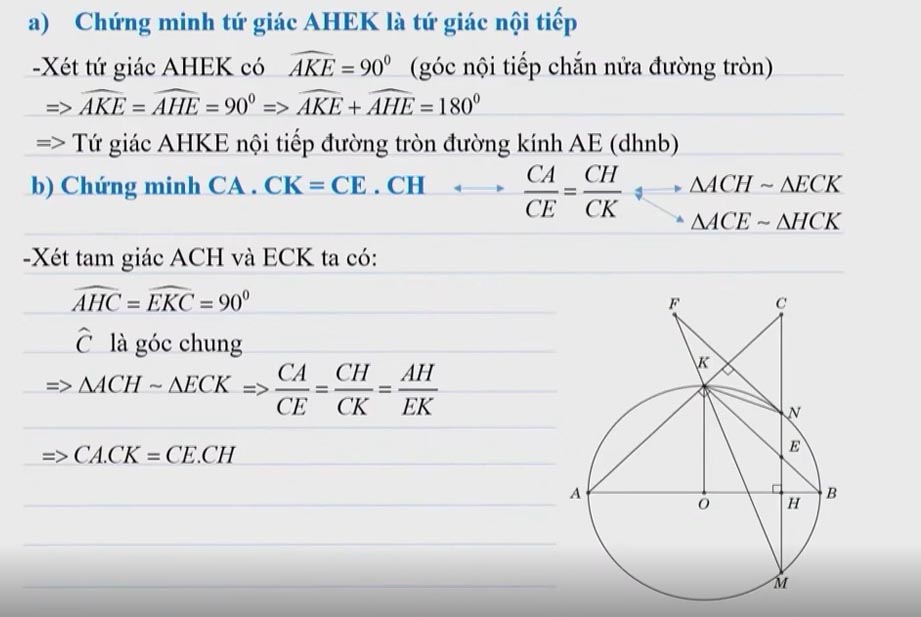
Ví dụ: Cho đường tròn (O; R) và điểm M cố định nằm ngoài (O;R). Từ M kẻ các tiếp tuyến MA, MB tới (O;R) (A, B là các tiếp điểm). Đường thẳng (d) bất kì qua M và cắt (O;R) tại hai điểm phân biệt C, D ( C nằm giữa M và D). Gọi N là giao điểm của AB và CD. Chứng minh tứ giác OAMB nội tiếp đường tròn.

2.2.2. Chứng minh tứ giác đã cho là hình bình hành, hình chữ nhật, hình thoi,…

Để chứng một tứ giác là hình bình hành, hình chữ nhật hoặc hình thoi, các bạn dựa vào những dấu hiệu nhận biết.

– Một tứ giác là hình bình hành khi:

+ Có các cạnh đối song song

+ Có các cạnh đối bằng nhau.

+Có hai cạnh đối song song và bằng nhau.

+ Có các góc đối bằng nhau.

– Một tứ giác là hình hình chữ nhật khi:

+ Có ba góc vuông.

+ Hình thang cân có một góc vuông.

+ Hình bình hành có một góc vuông.

+ Hình bình hành có hai đường chéo bằng nhau.

– Một tứ giác là hình thoi khi:

+ Có 4 cạnh bằng nhau.

+ Hình bình hành có hai cạnh kề bằng nhau.

+ Hình bình hành có hai đường chéo vuông góc nhau.

+ Hình bình hành có 1 đường chéo là đường phân giác của 1 góc.

2.2.3. Tiếp tuyến của đường tròn

Có 2 cách để chứng minh một đường thẳng là tiếp tuyến của đường tròn:

– Chứng minh đường tròn và đường thẳng có duy nhất 1 điểm chung.

– Chứng minh đường thẳng vuông góc với bán kính đường tròn tại tiếp điểm.

2.2.4. Chứng minh 3 điểm thẳng hàng

Ba điểm thẳng hàng được chứng minh bằng phương pháp:

– Chứng minh hai đường thẳng đi qua hai trong 3 điểm ấy và cùng vuông góc với đường đường thẳng thứ ba.

– Sử dụng hai góc kề bù có 3 điểm nằm trên hai tia đối nhau.

– Sử dụng tính chất đường phân giác của một góc.

– Sử dụng tính chất đường trung trực của đoạn thẳng.

– Sử dụng tính chất ba đường cao trong tam giác.

2.2.5. Chứng minh tỉ lệ độ dài đoạn thẳng

Khi tìm được mối liên hệ giữa các độ dài đoạn thẳng, bạn sẽ suy ra được tỉ lệ độ dài tương ứng để chứng minh.

3. Các cấu trúc đề thi vào 10 môn Toán

Căn cứ vào đề thi của 63 tỉnh thành, cấu trúc đề thi vào 10 môn Toán có thể được chia thành bốn nhóm như sau:

– Nhóm 1 (hay nhóm T1): với các yêu cầu ở mức độ cơ bản, câu hỏi thường cấp nhận biết hoặc thông hiểu

– Nhóm 2 (hay nhóm T2): với các yêu cầu ở mức khá, cần năng lực vận dụng tốt

– Nhóm 3: với các yêu cầu ở mức cao, dành riêng cho học sinh trên địa bàn Hà Nội

– Nhóm 4: cấu trúc đề theo xu hướng mới, yêu cầu học sinh vận dụng tốt kiến thức đã học vào giải các bài toán thực tế, dành riêng cho học sinh trên địa bàn thành phố Hồ Chí Minh

Những lưu ý quan trọng trong quá trình làm bài thi môn Toán 

– Chuẩn bị tâm lý tốt

Trong quá trình luyện thi, các bạn nên tập thói quen đặt thời gian làm bài như thi thật để có một tâm lý tốt khi làm bài thi thật. Bên cạnh đó, trước giờ thi không nên ôm đồm làm thêm đề, giải đề để tránh căng thẳng. Bên cạnh đó, học sinh nên đến phòng thi sớm để làm quen với không khí phòng thi, nói chuyện với các bạn cùng phòng để giữ tinh thần thoải mái trước khi bắt đầu thi.

– Đọc lướt toàn bộ đề thi và xác định thứ tự làm bài

Khi nhận được đề thi, việc đọc toàn bộ đề là việc quan trọng để các bạn xác định được thứ tự làm bài nhưng nhiều bạn lại bỏ qua dẫn đến việc mất thời gian ở những câu khó mà không biết có những câu dễ ở phía dưới. Thí sinh cần ưu tiên câu dễ làm trước, câu khó làm sau khi đã chắc chắn những câu chắc chắn “ăn điểm” ở trên.

– Không để mất điểm đáng tiếc

Trong quá trình làm bài thi môn Toán, có một số lỗi sai dưới đây mà các bạn học sinh tuyệt đối không được mắc phải để tránh mất điểm đáng tiếc khi làm bài thi:

+ Khi đọc đề, học sinh nên gạch chân những từ quan trọng bằng bút chì. Đặc biệt, không được viết sai đề, cần dành một phút kiểm tra đề mình viết vào giấy thi đã chính xác chưa.

+ Không trình bày ẩu, làm tắt bước.

+ Khi sửa, học sinh nên gạch chéo phần bị sai, rồi viết số hoặc chữ mới bên cạnh; không sửa bằng cách viết chồng lên phần đã sai. Lỗi này học sinh thường mắc.

Với những thông tin trên, chắc chắn cánh cửa vào ngôi trường THPT mơ ước của 2K9 sẽ càng mở rộng hơn nữa. Hi vọng sẽ giúp các bạn tích lũy đầy đủ kiến thức, kỹ năng và sự tự tin để vượt qua kỳ thi xuất sắc.